Greedy Coin-change Algorithm

Greedy selection-criteria: return largest coin that is less than or equal to the remaining change

Problem: Making 29-cents change with coins {1, 5, 10, 25, 50}

A 5-coin solution

Does this greedy algorithm always give the fewest number of coins?

Problem with Greedy Approach

Does not give the fewest coins for all coin sets.

Problem: Making 29-cents change with coins {1, 5, 10, 12, 25, 50}

This 5-coin solution is NOT optimal!

What solution would require the fewest coins?

Decrease-and-Conquer

Idea: Solve problem by:

• dividing it into small problem(s)
• solving the smaller problem(s)
• use solution(s) to smaller problem(s) to solve original problem

Consider the coin-change problem: Given a set of coin types and an amount of change to be returned, determine the fewest number of coins for this amount of change.

What determines the size of the problem?

How could we divide the coin-change problem for 29-cents into smaller problems?

If we knew the solution to these smaller problems, how would be able to solve the original problem?

Divide-and-Conquer Coin-change Solution

After we give back the first coin, then we have a smaller amount of change.

If we knew the fewest number of coins needed for each possible smaller problem, then how could determine the fewest number of coins needed for the original problem?

We can write a recursive relationship for the fewest number of coins as:

Problem with Divide-and-Conquer Solution

A lot of redundant calculations!!!

For coins of {1, 5, 10, 12, 25, 50}, typical timings:

Change Amount	Run-Time (seconds)
50	1
55	5
60	26
65	126
70	613

Exponential growth in run-time!

Dynamic Programming

Idea:

• Solve smaller problems before larger ones
• store their answers
• look-up answers to smaller problems when solving larger subproblems

Advantage:

Eliminates redundant work since each smaller problem solved only once!

Dynamic Programming Coin-change Solution

Fills an array fewestCoins from 0 to the amount of change

An element of fewestCoins stores the fewest number of coins necessary for the amount of change corresponding to its index value.

For 29-cents using the set of coin types {1, 5, 10, 12, 25, 50}: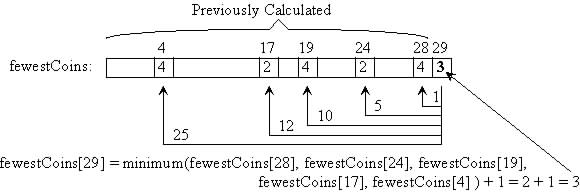

NOTICE: that the algorithm has previously calculated the fewestCoins for the change amounts of 0, 1, 2, ..., up to 28 cents.

Keeping Track of Coins in the Solution

If we record the best, first coin to return for each change amount (found in the "minimum" calculation) in an array bestFirstCoin, then we can easily recover the actual coin types to return.

For the 29-cent solution with coin types {1, 5, 10, 12, 25, 50}.

Possible Dynamic Programming Optimizations

1. Reduce execution-time by calculating only smaller problems needed

• Predictable pattern

  e.g., Calculation of binomial coefficient

• Irregular pattern - use memorization techique

  e.g., Knapsack problem

2. Reduce memory needed by reclaiming storage for no longer needed smaller problem solutions

e.g., Calculation of binomial coefficient