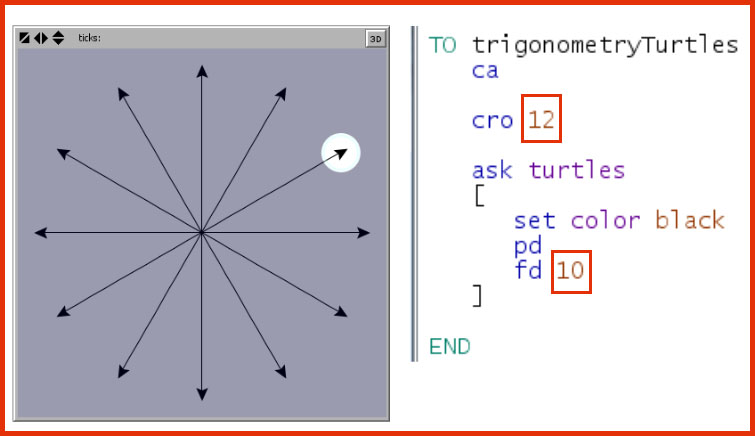
- The who numbers go from 0 to 11, clockwise, starting from the turtle that faces straight north, with heading of 0 degrees.
- It can easily be seen that there are 3 slices of pizza pie or pumpkin pie in the upper right quadrant or quarter of the NetLogo grid. Since this is 90 degrees of the entire 360, it is clear that each slice must be 30 degrees.
- Or you can divide 360 by 12, which gives you the degrees of the angle between each pair of lines they have drawn.
Whatever cro n cro n = create n ordered turtles value is, as in cro 32 or cro 8 or cro 36 or cro 72, the size of each slice is just 360 divided by n. 360 360 360 ----- = 10 ----- = 5 ----- = 30 36 72 12
i. What is known? Write down what is given.
Write down and determine what facts are
directly given or that can be derived from
what is stated or seen in the problem diagram.
Note: It can be VERY IMPORTANT for you to draw a diagram or picture of the situation.
It is NOT always given.
Or you might add to the picture that is given,
like I do below here for you (Photoshop).
This is your ammunition for trying to hit the target.
Your bow and arrows.
Or this is your fuel for taking you from the starting point
to the destination, from the given to the goal.
ii. What is unknown? What is the goal?
What is the result that is desired?
What is the question asking for?
That is your target!
That is your destination!
iii. How can you get from i. (given) to ii. (goal).
You now have a clear idea of where you are at,
and of where you want to go.
What formulas or past similar problem and trips
can help you get from i. to ii.?
You might need the SINE or COSINE or TANGENT.
Or for Monte Carlo you might need the
b
a = --- d formula.
c
rise
Or you might need the slope = --------
run
formula where rise = (y2 - y1)
and run = (x2 - x1)
etc. etc. etc.
Mobilize knowledge about circles, slopes,
right triangles, points, distances between
points, trigonometry that is relevant to
the current problem and the i. given facts
that you have WRITTEN DOWN and isolated and
the ii. relevant GOAL that you have also
WRITTEN DOWN as your clear target.
i. WHAT is given? Dr. Peter Venkman
WHAT is the goal?
ii. HOW to get from Dr. Raymond Stantz
i. given start to
ii. the desired result or goal.
iii. Solve the problem using whatever tools
(Netlogo, Vensim, calculator) and algebra
you need to do.
Dr. Egon Spengler
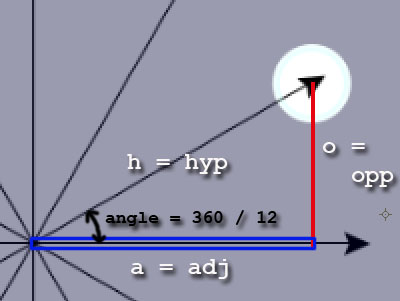
cosine(30) = adj/hyp = adj/10
Where does the 10 come from? The turtles each went forward 10 units! (fd 10)
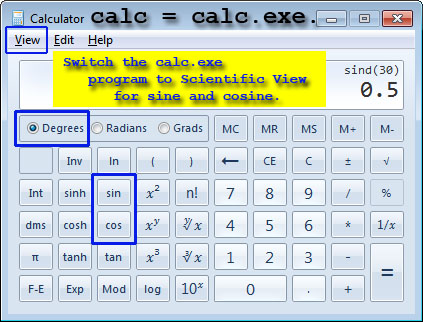
cosine(30) using the calculator calc.exe
show cosine of 30 degrees is 0.866.
0.866 = adj / 10 so multiply both sides
of the equation by 10,
we have:
(10)(0.866) = (10) (adj / 10) and 8.66 = adj, so the xcor answer is 8.66.
Remember to SHOW your WORK!!!! I am showing my work here, not just the final answer.
Sine(30) = OPP/HYP = OPP/10
Sine(30) = 0.5 = OPPOSITE / 10
and 10(0.5) = OPPOSITE = 5.0.
So the ycor is 5.0.
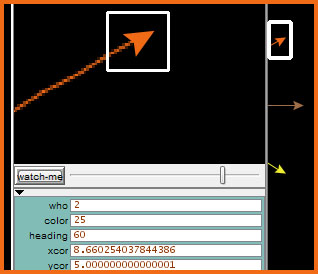
The (xcor, ycor) for the indicated turtle
with who number 2
is (8.66, 5.0)
Yes. Knowing the adjacent leg has length 8.66 units and knowing the angle is 30 degrees and having as our goal what is the length of the OPPosite Leg gives the following setup:
GIVEN GOAL
INPUT OUTPUT
i. ii.
Known or given: Goal, unknown to find, desired result:
-------------- -------------------------------------
Angle
30 degrees
Length of OPPosite side,
Adjacent side length opposite leg of the
8.66 units triangle, side opposite
the 30 degree angle.
How do you get from i. to ii. from given to goal?
TOA = Tangent Opposite Adjacent
Opposite opp O
Tangent = --------------- = ----- = --- Remember by thinking of
Adjacent adj A stubbing your TOA...
So the TOA formula is suggested when you focus on the fact
that you know the 30 degrees and can get the T Tangent, thus
with a calculator know the Tangent of 30 degrees,
and you know the length of the adjacent leg to the 30 degree
angle, which is 8.66.
opposite
Tan(30) = 0.57735 = ------------ so 8.66 * 0.57735 = opposite length
8.66
and 4.99985 - opposite length
thus 5.0 = ycor