- Some wow graphics to show you up front what R can do to help you visualize the patterns in your data:
> demo()
> demo(package = .packages(all.available = TRUE))
>
>
> demo(graphics)
demo(graphics)
---- ~~~~~~~~
Type to start :
- R and linear regression example.
- Using sequences, concatenate, etc.
> myVector<-c(11,22.2,33,44,55,66)
> myVector2 <- c(1.3, 1.4, 1.6, 1.75, 1.9, 2.1)
> seq(1,40,2)
[1] 1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39
> c<-seq(11,30,2)
> c
[1] 11 13 15 17 19 21 23 25 27 29
> d<-seq(1,20)
> d
[1] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
> d*2-1
[1] 1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39
> letters
[1] "a" "b" "c" "d" "e" "f" "g" "h" "i" "j" "k" "l" "m" "n" "o" "p" "q" "r" "s" "t" "u" "v"
[23] "w" "x" "y" "z"
- Postional arguments and named argument. pch is the NAME of an argument. Postional matching is used on 1st plot, both positional and named actual argument approach is used on the 2nd plot, and finally the 3rd plot uses only named actual arguments.
>
> plot(myVector,myVector2)
>
> plot(myVector,myVector2,pch=8)
> plot(pch=3,y=myVector2,x=myVector)
- Pages 83-84 of Peter Dalgaard Introductory Statistics with R - daily energy intake in kJ for 11 women.
> daily.intake <- c(5260,5470,5640,6180,6390,6515,6805,7515,7515,8230,8770)
> mean(daily.intake)
[1] 6753.636
> sd(daily.intake)
[1] 1142.123
> quantile(daily.intake)
0% 25% 50% 75% 100%
5260 5910 6515 7515 8770
> t.test(daily.intake,mu=7725)
One Sample t-test
data: daily.intake
t = -2.8208, df = 10, p-value = 0.01814
alternative hypothesis: true mean is not equal to 7725
95 percent confidence interval:
5986.348 7520.925
sample estimates:
mean of x
6753.636
- How do you get the data frames that are used in many of the R tutorials and that are used in the Peter Dalgaard book for all examples?
> library(ISwR)
energy, intake and juul are three of the many data sets in the ISwR library.
------ ------ ----
- Two-sample t test - daily energy expenditure comparisons - lean versus obese women study.
> data(energy)
> attach(energy)
> energy
expend stature
1 9.21 obese
2 7.53 lean
3 7.48 lean
4 8.08 lean
5 8.09 lean
6 10.15 lean
7 8.40 lean
8 10.88 lean
9 6.13 lean
10 7.90 lean
11 11.51 obese
12 12.79 obese
13 7.05 lean
14 11.85 obese
15 9.97 obese
16 7.48 lean
17 8.79 obese
18 9.69 obese
19 9.68 obese
20 7.58 lean
21 9.19 obese
22 8.11 lean
> t.test(expend~stature)
Welch Two Sample t-test
data: expend by stature
t = -3.8555, df = 15.919, p-value = 0.001411
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-3.459167 -1.004081
sample estimates:
mean in group lean mean in group obese
8.066154 10.297778
> t.test(expend~stature, var.equal=T)
Two Sample t-test
data: expend by stature
t = -3.9456, df = 20, p-value = 0.000799
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-3.411451 -1.051796
sample estimates:
mean in group lean mean in group obese
8.066154 10.297778
- Are the group variances the same? Using the var.test R function to test the equal variances assumption. Section 4.4 of Dalgaard book. Comparison of variances.
> var.test(expend~stature)
F test to compare two variances
data: expend by stature
F = 0.7844, num df = 12, denom df = 8, p-value = 0.6797
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
0.1867876 2.7547991
sample estimates:
ratio of variances
0.784446
- The paired t test examples.
> data(intake)
> attach(intake)
> intake
pre post
1 5260 3910
2 5470 4220
3 5640 3885
4 6180 5160
5 6390 5645
6 6515 4680
7 6805 5265
8 7515 5975
9 7515 6790
10 8230 6900
11 8770 7335
> post - pre
[1] -1350 -1250 -1755 -1020 -745 -1835 -1540 -1540 -725 -1330 -1435
> t.test(pre, post, paired=T)
Paired t-test
data: pre and post
t = 11.9414, df = 10, p-value = 3.059e-07
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
1074.072 1566.838
sample estimates:
mean of the differences
1320.455
> t.test(pre, post) # This is WRONG for above data!!!!
Welch Two Sample t-test
data: pre and post
t = 2.6242, df = 19.92, p-value = 0.01629
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
270.5633 2370.3458
sample estimates:
mean of x mean of y
6753.636 5433.182
- The juul data frame has 1,339 rows and 6 columns. IGF1 is Insulin-like Growth Factor. It is measured in mg/l, micrograms per liter.
> data(juul)
> attach(juul)
> mean(igf1)
[1] NA
> mean(igf1,na.rm=T)
[1] 340.168
> summary(igf1)
Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
25.0 202.2 313.5 340.2 462.8 915.0 321.0
- In R, the data sets NA's could be counted like this too, since TRUE is converted to 1 and FALSE is converted to 0 when we apply arithmetic operations or R functions that expect numeric input to TRUE and FALSE.
> sum(!is.na(igf1))
[1] 1018
> sum(is.na(igf1))
[1] 321
> 1018 + 321
[1] 1339 The juul data set is 1,339 rows and 6 columns...
- Making a variable categorical or a factor in R is often necessary.
> summary(juul)
age menarche sex igf1
Min. : 0.170 Min. : 1.000 Min. :1.000 Min. : 25.0
1st Qu.: 9.053 1st Qu.: 1.000 1st Qu.:1.000 1st Qu.:202.2
Median :12.560 Median : 1.000 Median :2.000 Median :313.5
Mean :15.095 Mean : 1.476 Mean :1.534 Mean :340.2
3rd Qu.:16.855 3rd Qu.: 2.000 3rd Qu.:2.000 3rd Qu.:462.8
Max. :83.000 Max. : 2.000 Max. :2.000 Max. :915.0
NA's : 5.000 NA's :635.000 NA's :5.000 NA's :321.0
tanner testvol
Min. : 1.000 Min. : 1.000
1st Qu.: 1.000 1st Qu.: 1.000
Median : 2.000 Median : 3.000
Mean : 2.640 Mean : 7.896
3rd Qu.: 5.000 3rd Qu.: 15.000
Max. : 5.000 Max. : 30.000
NA's :240.000 NA's :859.000
> juul$sex <- factor(juul$sex, labels=c("Male","Female"))
> summary(juul)
age menarche sex igf1
Min. : 0.170 Min. : 1.000 Male :621 Min. : 25.0
1st Qu.: 9.053 1st Qu.: 1.000 Female:713 1st Qu.:202.2
Median :12.560 Median : 1.000 NA's : 5 Median :313.5
Mean :15.095 Mean : 1.476 Mean :340.2
3rd Qu.:16.855 3rd Qu.: 2.000 3rd Qu.:462.8
Max. :83.000 Max. : 2.000 Max. :915.0
NA's : 5.000 NA's :635.000 NA's :321.0
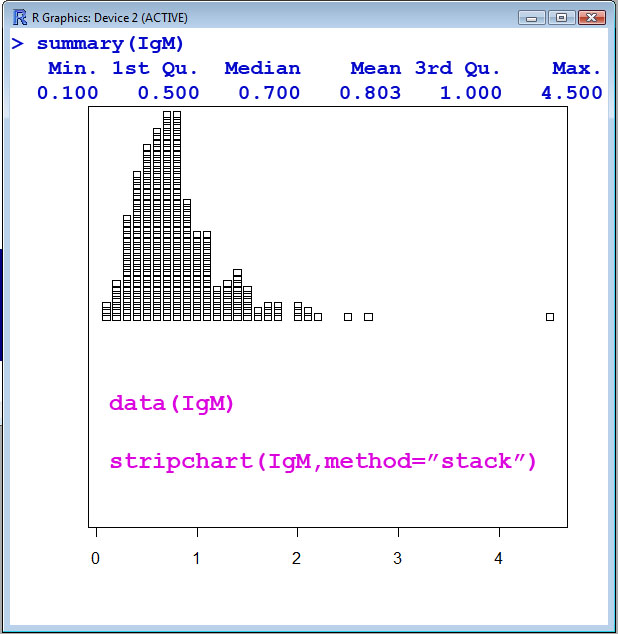
- The IgM data set is only a single column of data, i.e. a single numeric vector or a single variable. The Serum IgM (Immunoglobulin G) level in 298 children ranging in age from 6 months to 6 years. IgM is measured in gram/liter, i.e. g/l for the units.
> library(ISwR)
>
> data(IgM)
>
> stripchart(IgM,method="stack")
> summary(IgM)
Min. 1st Qu. Median Mean 3rd Qu. Max.
0.100 0.500 0.700 0.803 1.000 4.500
> sd(IgM)
[1] 0.4694982
>
> mean(IgM)
[1] 0.8030201
- ls() lists the contents of your workspace.
> ls()
[1] "b" "bmi" "bp.obese" "c" "caesar.shoe"
[6] "coking" "d" "daily.intake" "energy" "fake.trypsin"
[11] "heart.rate" "hh" "ht" "ht2" "IgM"
[16] "intake" "juul" "LETTERS" "m" "wt"
[21] "x" "xbar"
- Perhaps for class #2 or #3 use.
Hello R and RStudio students,
How to separate out a training data set of size 10,000
How to have all of the rest of the records be used for the
test data set.
Here is the code we did in today's class, after doing the code from
the textbook.
the trainIris data frame was 50 records from the iris dataset,
to be used for training.
The testIris data frame was the other 100 records from the iris
dataset.
You can use either the cbind() method or the data.frame() function.
Do ?sample() and do ?data.frame() and do ?cbind() if you want to
learn more about them
# March 6th, 2018 Tuesday
i.data <- iris
sample(1:nrow(i.data), nrow(i.data))
sort(sample(1:20, 10, replace=TRUE)) # Luckily replace=FALSE is the DEFAULT.
s <- sample(1:nrow(i.data), nrow(i.data))
sdframe <- data.frame(s) # the s permutation of 150 values
# has to be converted to data frame first
myData <- data.frame(sdframe, iris) # way number one
myData2 <- cbind( iris, s ) # way number two - this way can handle s
sort(s)
s
trainIris <- myData[myData$s<=50, ]
head(trainIris)
tail(trainIris)
s
testIris <- myData[myData$s > 50, ]
permute <- sample(1:20, 20) # creates a permutation of the set 1:20
sort(permute)