Section 1.2 and Section 1.3
Materials
From Section 1.2
Vocabulary
Key Idea
- When evaluating a compount proposition that contains more than one logic operator you must make sure to follow the proper "order of operations"
- For logical operators this is:
- Notice that if we consider conjunction to be related to multiplication and disjunction related to addition (as we discussed with Section 1.1) than this is exactly the same order of operations that we use with arithmetic
From Section 1.3
Vocabulary
- conditional operation (⇒or →)
- conditional proposition
- conditional statement
- hypothesis (antecedent)
- conclusion (consequent)
- converse
- contrapositive
- inverse
- biconditional operation (⇔ or ↔)
Key Ideas
- The conditional operation is like the "if then" in programming. It indicates that when a certain condition is met (called the hypothesis or antecedent) then a certain result must occur (called the conclusion or consequent).
- It's truth table looks like:
-
| p |
q |
p → q |
| T |
T |
T |
| T |
F |
F |
| F |
T |
T |
| F |
F |
T |
- The biggest mistake students make with the conditional operator is marking it false when the condition is false. This is incorrect.
- The other way to think about the conditional operator is to remember that p ⇒ q ≡
 p
p 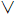 q
q
- The other common mistake(s) people make are starting with a conditional statement and assuming its converse or inverse.
- An original conditional statement is only equivalent to it's contrapositive.
- The converse and inverse are equivalent TO EACH OTHER but are not the same as the original conditional or it's contrapositive.
- The biconditional operation is like a conditional statement that is true in both directions.
- That is, if p ⇒ q and q ⇒p then we say that p ⇔ q