CS 3540 Homework 2

According to The Joy of Cooking, when you are cooking candy syrups, you should cook them 1 degree cooler than listed in the recipe for every 500 feet of elevation you are above sea level. For example, the recipe for Chocolate Carmels calls for a temperature of 244° Fahrenheit. If you were making your Chocolate Carmels in Denver, the Mile-High City, you would want to cook the syrup at 233.44°.
Write a Racket function named candy-temperature that takes two arguments, the recipe's temperature in degrees Fahrenheit and the elevation in feet, and returns the temperature to use at that elevation. For example:
```
     > (candy-temperature 244 5280)    ;; Denver, baby!
     233.44
     > (candy-temperature 302 977.69)  ;; the highest point in Cedar Falls
     300.04462                         ;;     is approx. 298m above sea level
     > (candy-temperature 302 -1401)   ;; the Dead Sea 1401 ft below sea level
     304.802
```

A 10-foot ladder leans against a wall. If its base is 6 feet away from the bottom of the wall, then it reaches 8 feet high on the wall. This is a simple example of the Pythagorean theorem.
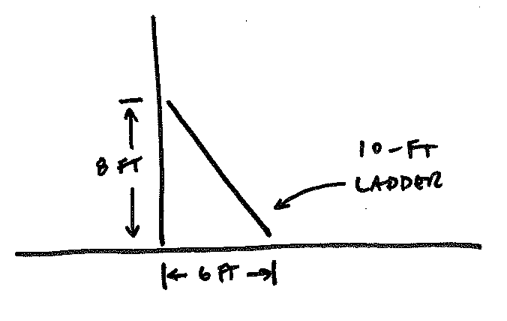
Write a Racket function named ladder-height that takes two arguments, the length of the ladder and the distance at the base. Both are in feet. The function returns the distance up the wall reached by the ladder, also in feet. For example:
```
     > (ladder-height 10 6)
     8
     > (ladder-height 13 5)
     12
     > (ladder-height 20 3.5)     ; that's steep... be careful!!
     19.691368667515217
```
You may want to create a function to square a number, and use it to compute the ladder's height.

I walk two miles to work every morning during the winter, so I pay close attention to the wind chill. According to Wikipedia, we can approximate the wind chill to within one degree using this formula:
```
     T_wc = 35.74 + 0.6215·T_a - 35.75·V^0.16 + 0.4275·T_a·V^0.16
```
where T_wc is the wind chill index in degrees Fahrenheit, T_a is the air temperature in degrees Fahrenheit, and V is the wind speed in miles/hour.
Write a Racket function named wind-chill that takes two arguments, the air temperature in degrees Fahrenheit and the wind speed in miles/hour, and returns the corresponding wind chill index. For example:
```
     > (wind-chill 0 5)
     -10.509947791689996
     > (wind-chill 40 5)
     36.47240485832117
     > (wind-chill 35 15)
     25.43151479664407
     > (wind-chill -10 25)     ; one morning this winter...
     -37.46372963656345
```
The wind chill formula uses V^0.16 in two places. Rather than computing that value twice, this is the perfect place to compute it once and give the result a name using a let expression. You may do so if you like!

Write Racket functions named +mod, -mod, and *mod that perform modular addition, subtraction, and multiplication. Each function should take three arguments: two integers to combine, i and j, and a modulus n. For example:
```
     > (+mod 2 3 12)
     5
     > (-mod 9 18 12)
     3
     > (*mod 6 5 12)
     6
     > (+mod 10 10 3)
     2
     > (-mod 121 104 13)
     4
     > (*mod 6 6 9)
     0
```

Generally, the dimensions of engineered components are not exactly the specified value, but rather within a certain tolerance of the specified value. The tolerance generally depends upon the application and the material being used. For example, a metal piece used in construction that is listed as 5 cm in length might actually be any length within 1 mm of 5 cm, that is, between 4.9 cm and 5.1 cm, inclusive.
Write a Racket procedure named in-range? that takes three numbers as arguments: two numbers to compare, and a tolerance, epsilon. in-range? returns true if its first two arguments are within epsilon of one another, and false otherwise. For example:
```
     > (in-range? 4.95 5.0 0.1)
     #t
     > (in-range? 4.95 5.0 0.01)    ;; not anymore!
     #f
     > (in-range? 5.0 4.95 0.1)     ;; works both ways
     #t
     > (in-range? 5.0 5.95 0.1)
     #f
     > (in-range? 5.5 5.95 0.5)
     #t
```