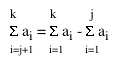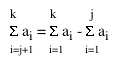TITLE: Proofs from THE BOOK
AUTHOR: Eugene Wallingford
DATE: October 01, 2004 2:04 PM
DESC: Proofs from THE BOOK is a great read if you like math and creative thinking.
-----
BODY:
I just finished reading Proofs from THE BOOK, by Martin
Aigner and Günter Ziegler. The title comes from Paul
Erdós, who "liked to talk about The Book, in which
God maintains the perfect proofs for mathematical theorems".
Mathematicians don't have to believe in God, said Erdós,
but they have to believe in the book. Proofs from THE BOOK
collects some of the proofs Erdós liked best and some
others in the same spirit: clever or elegant proofs that reflect
some interesting insight into a problem.
I am a computer scientist, not a mathematician, but many of these
proofs made me smile. My favorite sections were on number theory
and combinatorics. Some of the theorems on prime and irrational
numbers were quite nice.
My favorite proof from The Book applied the pigeonhole principle
in a surprising way. The claim:
Suppose we are given n integers a1, ..., an,
which need not be distinct. Then there is always a set of consecutive
numbers aj+1, ..., ak whose sum is a multiple
of n.
This doesn't seem obvious to me at all. But consider the sequences
N = {0, a1, a1+a2,
a1+a2+a3, ...,
a1+a2+...+an} and
R = {0, 1, 2, ..., n-1}. Now consider the function f that maps
each member of N, ai, to (ai mod n) in R.
Now, |N| = n+1 and |R| = n, so by the pigeonhole principle we know
that there must be two sums from N, a1+...+aj
and a1+...+ak (j<k), mapped to the same
value in R. a1+...+aj may actually be 0,
the first value in N, but that doesn't affect our result.
Then:
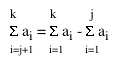must have a remainder of 0. QED. Beautiful.
Eugene sez: Check out Proofs from THE BOOK.
P.S. It might be fun to create a similar book for proofs related
specifically to computer science. Proofs from THE BOOK
has some proofs on counting and one proof on information theory,
but most of the book focuses on mathematics more broadly.
-----