TITLE: A Programming Digression: Farey Sequences
AUTHOR: Eugene Wallingford
DATE: October 25, 2010 4:50 PM
DESC:
-----
BODY:
 Last Wednesday, I saw John Cook's article on
rational approximations using Farey's algorithm,
and it led me on a programming journey. You might find
it entertaining.
First, some background. The students in my compilers
course are writing a compiler for a simple numerical
language I call Klein. Klein is a minimal functional
language inspired by
Doug Baldwin's
MinimL, designed to give compiler students experience
with all the important issues in the course while
not duplicating very much. The goal is that students
be able to write a complete and correct compiler for
the language from scratch in a semester. Among Klein's
limitations are:
Last Wednesday, I saw John Cook's article on
rational approximations using Farey's algorithm,
and it led me on a programming journey. You might find
it entertaining.
First, some background. The students in my compilers
course are writing a compiler for a simple numerical
language I call Klein. Klein is a minimal functional
language inspired by
Doug Baldwin's
MinimL, designed to give compiler students experience
with all the important issues in the course while
not duplicating very much. The goal is that students
be able to write a complete and correct compiler for
the language from scratch in a semester. Among Klein's
limitations are:
- Repetition is done with recursion. There are
no loops.
- There are only two data types, integers and
booleans.
- All binding of values to names is done via
function calls. There are no local variables,
no assignments statements, and no sequences.
- There is only one primitive function, print,
that can be called only at the top of a function
definition.
As you can imagine, it is difficult to find good, large
problems for which we can write Klein programs. So I'm
always on the look-out for numerical algorithms that can
be implemented in Klein.
When I saw Cook's article and Python program, I got to
thinking... Wouldn't this be a cool application for
Klein?
Of course, I faced a few problems. Cook's program takes
as arguments a real number in [0..1), r,
and an integer N. It returns a fraction
that is the rational number closest in value to
r with a denominator that no bigger than
N. Klein does not have floating-point
values, so I would have to fake even the real value
being approximated! Without assignment statements and
sequences of statements, let alone Python's multiple
assignments and multiple returns, I would have to convert
the algorithm's loop to a set of functions for computing
the individual components of the converging bounds.
Finally, without floats again, I would also have to
compare the bounding fractions to the faked real number
as fractions.
Those are just the sort of challenges that intrigue a
programmer. I spent a couple of hours on Thursday
slowly refactoring Cook's code to a Klein-like subset
of Python. Instead of passing r to the
main function, I fake it by passing in two arguments: the
digits to the right of the decimal point as an integer,
and a power of 10 to indicate its magnitude. These serve
as numerator and denominator of a rational approximation,
albeit with a very denominator. For example, r
= 0.763548745, I pass in 7635487 and 10,000,000. The
third argument to the function is N. Here
is an example:
>>> farey( 127, 1000, 74)
8
63
8/63 is the best rational approximation for 0.127 with a
denominator ≤ 74. My code prints the 8 and returns
the 63, because that is best way for an equivalent Klein
program to work.
Here is Cook's example of 1/e with a denominator
bounded by 100:
>>> farey( 367879, 1000000, 100 )
32
87
Take a look at
my Python code
if you are easily amused. In one part of the program, I
duplicated code with only small changes to the resulting
functions, farey_num() andfarey_den.
In another section, I avoided creating duplicate functions
by adding a selector argument that I allowed me to use one
bit of code for two different calculations. while_loop_for
returns the next value for one of a, b,
c, and d, depending on the value of its
first argument. For some reason, I am fond of the code
that replaces Cook's mediant variable.
At this point, the
port to Klein
was straightforward.
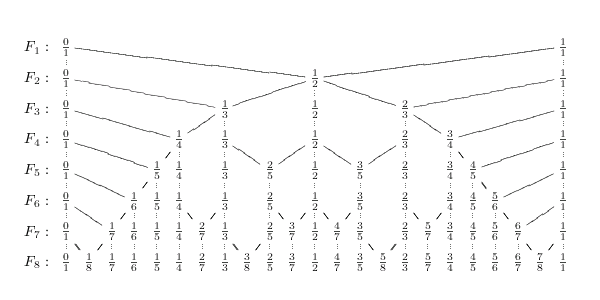
In the end, there is so much code to do what is basically
a simple task: to compute row N of this
tree on an as-needed basis, in the service of a binary
search:
 Programming in Klein feels a lot like programming in an
integer assembly language. That can be an interesting
experience, but the real point of the language is to
exercise students as they write a compiler. Still, I
find myself now wanting to implement refactoring support
for Klein, in order to make such digressions flow faster
in the future!
I enjoyed this little diversion so much that I've been
buttonholing every colleague who walks through the door.
I decided I'd do the same to you.
-----
Programming in Klein feels a lot like programming in an
integer assembly language. That can be an interesting
experience, but the real point of the language is to
exercise students as they write a compiler. Still, I
find myself now wanting to implement refactoring support
for Klein, in order to make such digressions flow faster
in the future!
I enjoyed this little diversion so much that I've been
buttonholing every colleague who walks through the door.
I decided I'd do the same to you.
-----

 Last Wednesday, I saw John Cook's article on
rational approximations using Farey's algorithm,
and it led me on a programming journey. You might find
it entertaining.
First, some background. The students in my compilers
course are writing a compiler for a simple numerical
language I call Klein. Klein is a minimal functional
language inspired by
Doug Baldwin's
MinimL, designed to give compiler students experience
with all the important issues in the course while
not duplicating very much. The goal is that students
be able to write a complete and correct compiler for
the language from scratch in a semester. Among Klein's
limitations are:
Last Wednesday, I saw John Cook's article on
rational approximations using Farey's algorithm,
and it led me on a programming journey. You might find
it entertaining.
First, some background. The students in my compilers
course are writing a compiler for a simple numerical
language I call Klein. Klein is a minimal functional
language inspired by
Doug Baldwin's
MinimL, designed to give compiler students experience
with all the important issues in the course while
not duplicating very much. The goal is that students
be able to write a complete and correct compiler for
the language from scratch in a semester. Among Klein's
limitations are:
