This morning, John Cook posted a blog entry on
the leading digits of factorials
and how, despite what might be our intuition, they follow
Benford's Law.
He whipped up some Python code and showed the results of
his run for factorials up to 500. I have linked to his
graphic at the right.
As I am
,
I decided to whip up a quick Scheme version of Cook's
experiment. He mentioned some implementation issues
involving the sizes of integers and floating-point numbers
in Python, and I wondered how well Scheme would fare.
For my first attempt, I did the simplest thing that would
possibly work. I already had a tail-recursive
factorial function and so wrote a procedure that
would call it n times and record the first digit
of each:
(define benford-factorials
(lambda (n)
(let ((counts (make-vector 10 0)))
(letrec ((foreach
(lambda (n)
(if (zero? n)
counts
(let ((lead-digit (first-digit (factorial n))))
(vector-set! counts lead-digit
(+ 1 (vector-ref counts lead-digit)))
(foreach (- n 1)))))))
(foreach n)))))
This gets the answers for us:
> (benford-factorials 500)
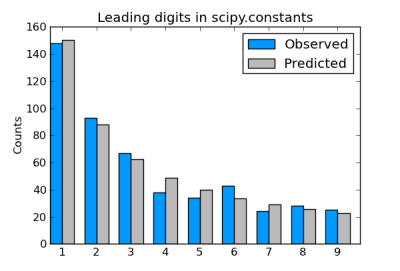
#(0 148 93 67 38 34 43 24 28 25)
Of course, it is wildly inefficient. My naive implementation
computes and acts on each factorial independently, which means
that it recomputes (n-1)!, (n-2)!, ... for each
value less than n. As a result, benford-factorials
becomes unnecessarily sluggish for even relatively small values
of n. How can I do better?
I decided to create a new factorial function, one that caches
the smaller factorials it creates on the way to n!. I
call it all-factorials-up-to:
(define all-factorials-up-to
(lambda (n)
(letrec ((aps (lambda (i acc)
(if (> i n)
acc
(aps (+ i 1)
(cons (* i (car acc)) acc))))))
(aps 2 '(1)))))
Now, benford-factorials can use a more functional
approach: map first-digit over the list of factorials,
and then map a count incrementer over the list of first digits.
(define benford-factorials
(lambda (n)
(let ((counts (make-vector 10 0))
(first-digits (map first-digit
(all-factorials-up-to n))))
(map (lambda (digit)
(vector-set! counts digit
(+ 1 (vector-ref counts digit))))
first-digits)
counts)))
(We can, of course, do without the temporary variable
first-digit by dropping the first map
right into the second. I often create
an explaining temporary variable
such as this one to make my code easier for me to write
and read.)
How does this one perform? It gets the right answers and
runs more comfortably on larger n:
> (benford-factorials 500)
#(0 148 93 67 38 34 43 24 28 25)
> (benford-factorials 1000)
#(0 293 176 124 102 69 87 51 51 47)
> (benford-factorials 2000)
#(0 591 335 250 204 161 156 107 102 94)
> (benford-factorials 3000)
#(0 901 515 361 301 244 233 163 147 135)
> (benford-factorials 4000)
#(0 1192 707 482 389 311 316 227 201 175)
> (benford-factorials 5000)
#(0 1491 892 605 477 396 387 282 255 215)
This procedure begins to be sluggish for n ≥ 3000
on my iMac.
Cook's graph shows how closely the predictions of Benford's
Law fit for factorials up to 500. How well do the actual
counts match the predicted values for the larger sets of
factorials? Here is a comparison for n = 3000, 4000,
and 5000:
n = 3000
digit 1 2 3 4 5 6 7 8 9
actual 901 515 361 301 244 233 163 147 135
predicted 903 528 375 291 238 201 174 153 137
n = 4000
digit 1 2 3 4 5 6 7 8 9
actual 1192 707 482 389 311 316 227 201 175
predicted 1204 704 500 388 317 268 232 205 183
n = 5000
digit 1 2 3 4 5 6 7 8 9
actual 1491 892 605 477 396 387 282 255 215
predicted 1505 880 625 485 396 335 290 256 229
That looks pretty close to the naked eye. I've always found
Benford's Law to be almost magic, even though mathematicians
can give a reasonable account of why it holds. Seeing it
work so well with something seemingly as arbitrary as
factorials only reinforces my sense of wonder.
If you would like play with these ideas, feel free to start
with
my Scheme code.
It has everything you need to replicate my results above. If
you improve on my code or take it farther, please
let me know!
-----