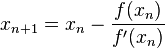TITLE: A Programming Digression: Generating Excellent Numbers AUTHOR: Eugene Wallingford DATE: December 08, 2015 3:55 PM DESC: ----- BODY: Background Whenever I teach my compiler course, it seems as if I run across a fun problem or two to implement in our source language. I'm not sure if that's because I'm looking or because I'm just lucky to read interesting blogs and Twitter feeds.
Farey sequences as Ford circles
For example, during a previous offering, I read on John Cook's blog about Farey's algorithm for approximating real numbers with rational numbers. This was a perfect fit for the sort of small language that my students were writing a compiler for, so I took a stab at implementing it. Because our source language, Klein, was akin to an integer assembly language, I had to unravel the algorithm's loops and assignment statements into function calls and if statements. The result was a program that computed an interesting result and that tested my students' compilers in a meaningful way. The fact that I had great fun writing it was a bonus. This Semester's Problem Early this semester, I came across the concept of excellent numbers. A number m is "excellent" if, when you split the sequence of its digits into two halves, a and b, b² - a² equals n. 48 is the only two-digit excellent number (8² - 4² = 48), and 3468 is the only four-digit excellent number (68² - 34² = 3468). Working with excellent numbers requires only integers and arithmetic operations, which makes them a perfect domain for our programming language. My first encounter with excellent numbers was Brian Foy's Computing Excellent Numbers, which discusses ways to generate numbers of this form efficiently in Perl. Foy uses some analysis by Mark Jason Dominus, written up in An Ounce of Theory Is Worth a Pound of Search, that drastically reduces the search space for candidate a's and b's. A commenter on the Programming Praxis article uses the same trick to write a short Python program to solve that challenge. Here is an adaptation of that program which prints all of the 10-digit excellent numbers: 
    for a in range(10000, 100000):
        b = ((4*a**2+400000*a+1)**0.5+1) / 2.0
        if b == int(b):
           print( int(str(a)+str(int(b))) )
I can't rely on strings or real numbers to implement this in Klein, but I could see some alternatives... Challenge accepted! My Standard Technique We do not yet have a working Klein compiler in class yet, so I prefer not to write complex programs directly in the language. It's too hard to get subtle semantic issues correct without being able to execute the code. What I usually do is this: This produces what I hope is a semantically correct program, using only primitives available in Klein. Finally, I translate the Python program into Klein and run it through my students' Klein front-ends. This parses the code to ensure that it is syntactically correct and type-checks the code to ensure that it satisfies Klein's type system. (Manifest types is the one feature Klein has that Python does not.) As mentioned above, Klein is something like integer assembly language, so converting to a Klein-like subset of Python means giving up a lot of features. For example, I have to linearize each loop into a sequence of one or more function calls, recursing at some point back to the function that kicks off the loop. You can see this at play in my Farey's algorithm code from before. I also have to eliminate all data types other than booleans and integers. For the program to generate excellent numbers, the most glaring hole is a lack of real numbers. The algorithm shown above depends on taking a square root, getting a real-valued result, and then coercing a real to an integer. What can I do instead?
the iterative step in Newton's method
Not to worry. sqrt is not a primitive operator in Klein, but we have a library function. My students and I implement useful utility functions whenever we encounter the need and add them to a file of definitions that we share. We then copy these utilities into our programs as needed. sqrt was one of the first complex utilities we implemented, years ago. It uses Newton's method to find the roots of an integer. For perfect squares, it returns the argument's true square root. For all other integers, it returns the largest integer less than or equal to the true root. With this answer in hand, we can change the Python code that checks whether a purported square root b is an integer using type coercion: 
    b == int(b)
into Klein code that checks whether the square of a square root equals the original number: 
    isSquareRoot(r : integer, n : integer) : boolean
      n = r*r
(Klein is a pure functional language, so the return statement is implicit in the body of every function. Also, without assignment statements, Klein can use = as a boolean operator.) Generating Excellent Numbers in Klein I now have all the Klein tools I need to generate excellent numbers of any given length. Next, I needed to generalize the formula at the heart of the Python program to work for lengths other than 10. For any given desired length, let n = length/2. We can write any excellent number m in two ways: If we set the two m's equal to one another and solve for b, we get: 
        1
    b = -(1 + sqrt[4a2 + 4(10n)a + 1])
        2
Now, as in the algorithm above, we loop through all values for a with n digits and find the corresponding value for b. If b is an integer, we check to see if m = ab is excellent. The Python loop shown above works plenty fast, but Klein doesn't have loops. So I refactored the program into one that uses recursion. This program is slower, but it works fine for numbers up to length 6: 
    > python3.4 generateExcellent.py 6
    140400
    190476
    216513
    300625
    334668
    416768
    484848
    530901
Unfortunately, this version blows out the Python call stack for length 8. I set the recursion limit to 50,000, which helps for a while... 
    > python3.4 generateExcellent.py 8
    16604400
    33346668
    59809776
    Segmentation fault: 11
Cool. Next Step: See Spot Run The port to an equivalent Klein program was straightforward. My first version had a few small bugs, which my students' parsers and type checkers helped me iron out. Now I await their full compilers, due at the end of the week, to see it run. I wonder how far we will be able to go in the Klein run-time system, which sits on top of a simple virtual machine. If nothing else, this program will repay any effort my students make to implement the proper handling of tail calls! That will be worth a little extra-credit... This programming digression has taken me several hours spread out over the last few weeks. It's been great fun! The purpose of Klein is to help my students learn to write a compiler. But the programmer in me has fun working at this level, trying to find ways to implement challenging algorithms and then refactoring them to run deeper or faster. I'll let you know the results soon. I'm either a programmer or crazy. Probably both. -----