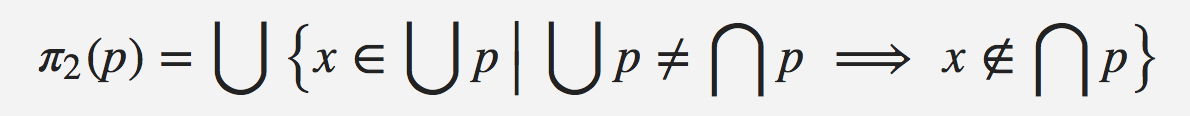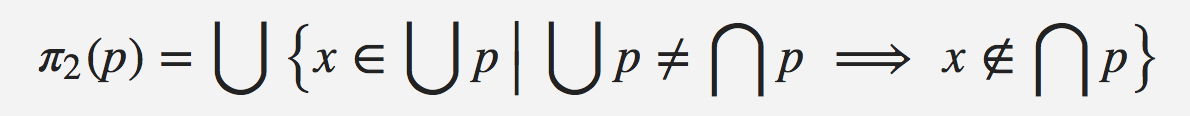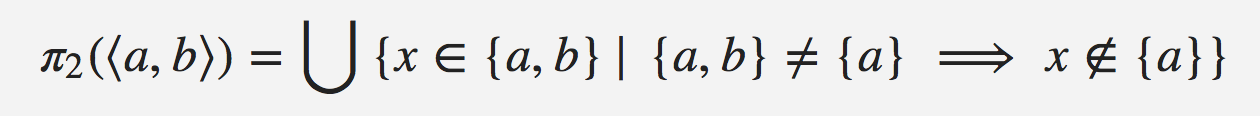TITLE: More Fun, Better Code: A Bug Fix for my Pair-as-Set Implementation
AUTHOR: Eugene Wallingford
DATE: April 16, 2022 2:32 PM
DESC:
-----
BODY:
In
my previous post,
I wrote joyously of a fun bit of programming: implementing ordered
pairs using sets.
Alas, there was a bug in my solution. Thanks to
Carl Friedrich Bolz-Tereick
for finding it so quickly:
Heh, this is fun, great post! I wonder what happens though if a = b?
Then the set is {{a}}. first should still work, but would second fail,
because the set difference returns the empty set?
Carl Friedrich had found a hole in my small set of tests, which
sufficed for my other implementations because the data structures I
used separate cells for the first and second parts of the pair. A
set will do that only if the first and second parts are different!
Obviously, enforcing a != b is unacceptable. My first code
thought was to guard second()'s behavior:
if my formula finds a result
then return that result
else return (first p)
This feels like a programming hack. Furthermore, it results in an
impure implementation: it uses a boolean value and an if
expression. But it does seem to work. That would have to be good
enough unless I could find a better solution.
Perhaps I could use a different representation of the pair. Helpfully,
Carl Friedrich followed up with
pointers to several blog posts
by Mark Dominus from last November that looked at the set encoding of
ordered pairs in some depth.
One of those posts
taught me about another possibility: Wiener pairs. The idea is this:
(a,b) = { {{a},∅}, {{b}} }
Dominus shows how Wiener pairs solve the a == b edge case in
Kuratowski pairs, which makes it a viable alternative.
Would I ever have stumbled upon this representation, as I did onto the
Kuratowski pairs? I don't think so. The representation is more
complex, with higher-order sets. Even worse for my implementation, the
formulas for first() and second() are much more
complex. That makes it a lot less attractive to me, even if I never
want to show this code to my students. I myself like to have a solid
feel for the code I write, and this is still at the fringe of my
understanding.
Fortunately, as I read more of Dominus's posts, I found there might be
a way to save my Kuratowski-style solution. It turns out that the
if expression I wrote above parallels the set logic used to
implement a second() accessor for Kuratowski pairs: a choice
between the set that works for a != b pairs and a
fallback to a one-set solution.
From
this Dominus post,
we see the correct set expression for second() is:
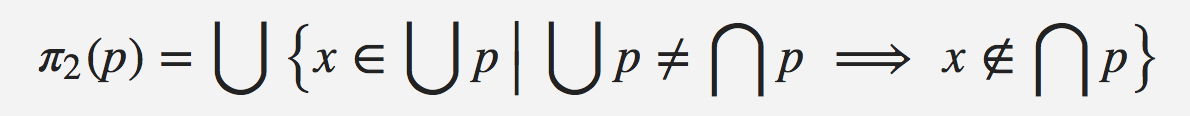... which can be simplified to:
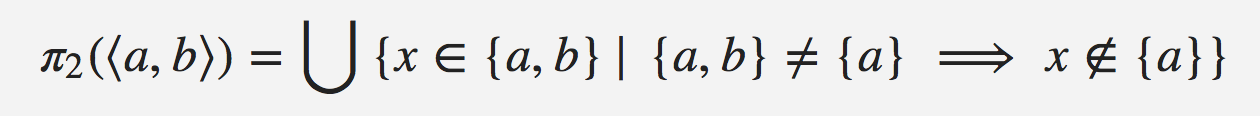The latter expression is useful for reasoning about second(),
but it doesn't help me implement the function using set operations.
I finally figured out what the former equation was saying: if
(∪ p) is same as (∩ p), then
the answer comes from (∩ p); otherwise, it comes
from their difference.
I realized then that I could not write this function purely in terms
of set operations. The computation requires the logic used to make
this choice. I don't know where the boundary lies between pure set
theory and the logic in the set comprehension, but a choice based on
a set-empty? test is essential.
In any case, I think I can implement the my understanding of the set
expression for second() as follows. If we define
union-minus-intersection as:
(set-minus (apply set-union aSet)
(apply set-intersect aSet))
then:
(second p) = (if (set-empty? union-minus-intersection)
(set-elem (apply set-intersect aSet))
(set-elem union-minus-intersection))
The then clause is the same as the body of first(), which
must be true: if the union of the sets is the same as their
intersection, then the answer comes from the interesection, just as
first()'s answer does.
It turns out that this solution essentially implements my first code
idea above: if my formula from the previous blog entry finds a result,
then return that result. Otherwise, return first(p). The
circle closes.
Success! Or, I should: Success!(?) After having a bug in my
original solution, I need to stay humble. But I think this does it.
It passes all of my original tests as well as tests for
a == b, which is the main edge case in all the discussions I
have now read about set implementations of pairs. Here is a link to
the final code file,
if you'd like to check it out. I include the two simple test scenarios,
for both a == b and a == b, as Rackunit tests.
So, all in all, this was a very good week. I got to have some fun
programming, twice. I learned some set theory, with help from a
colleague on Twitter. I was also reacquainted with Mark Dominus's
blog, the RSS feed for which I had somehow lost track of. I am glad
to have it back in my newsreader.
This experience highlights one of the selfish reasons I like for students
to ask questions in class. Sometimes, they lead to learning and enjoyment
for me as well. (Thanks, Henry!) It also highlights one of the reasons
I like Twitter. The friends we make there participate in our learning
and enjoyment. (Thanks, Carl Friedrich!)
-----