Intelligent agents sometimes act by reflex, and sometimes they act by looking up the right answer. But these behaviors work only in limited environments -- environments that are simple, static, or both. How can an agent choose an action in a complex environment, trying to achieve a goal that it knows little about? One approach is to search for an answer. An agent can consider what effect each possible action would have on the world and which action -- or sequence of actions -- leads to the goal.
We might expect an intelligent agent to consider its options in a systematic way, in a way that makes some sense, either logically or based on its knowledge of the world. For now, let's consider agents that act logically, but with relatively little knowledge about the the goal it is trying to achieve. XS
This algorithm describes a systematic way to search for an action, without yet committing to the system it will use:
In a nutshell, this algorithm says to keep considering possible states of the world until you find one that matches your goal. When you find one that does, do the actions that will take you to the desired state. How will you know what those actions are? Each time you look at a state and see that it isn't our goal, add all the states that you can get to from that state to the set of things to be considered.
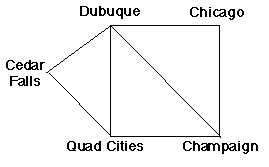
Consider how a program might search a map to find a route to where it wants to be. Next week, when I go to my conference, I must travel from Cedar Falls to the Champaign, Illinois, area. I have decided to drive, so I have to negotiate this simplified map:

In order to apply our algorithm, we need to define this problem in the vocabulary of search:
When we apply our search algorithm, we have to provide a "search strategy", which tells us how to choose a state from the set of unexplored states. This strategy acts as a bias toward a certain kind of state, as is the primary way that we can control the general direction of the algorithm.
We can use this algorithm to simulate the sort of random search we talked about last time. We could give the algorithm a strategy with no bias on the order we consider the states: choose a state randomly from the set. How successful is this algorithm likely to be?
A simple bias that we could give the algorithm is a bias toward "old" states, those states added to the set earliest. Using this approach, which path will the algorithm choose to Champaign? When do you imagine that this sort of bias is a good one to have?
To implement this in a program, we could represent the set of unexplored states as a list, sorted in ascending operators on the number of steps it takes to reach each state.
Another simple bias that we could give the algorithm is a bias toward "new" states, those states added to the set last. Using this approach, which path will the algorithm choose to Champaign? When do you imagine that this sort of bias is a good one to have?
To implement this in a program, we could represent the set of unexplored states as a list, sorted in descending operators on the number of steps it takes to reach each state.
Now that we have at least two reasonable search strategies available to us, we have to be able to figure out what their strengths and weaknesses are. That way, when faced with a particular problem, we (or our program!!) will be able to make a good choice of search strategy to use.
Four important criteria that can be used to evaluate a search strategy are:
The first strategy we considered above, a bias toward old states, is usually called breadth-first search, because it will consider all states at one distance from the initial state before it considers any states farther away.
How does BFS stack up against our evaluation criteria?
The expensiveness of BFS is a product of the problem's branching factor. If there aren't many operators available in a given state, then the cost of BFS can be low. But... for most problems in the world, an agent has many operators available at any time. And, even worse, finding a goal usually requires a long sequence of actions, which means that the agent must search deep into the "tree" of possibilities.
A strategy with a bias toward old states is called depth-first, because it will consider all solutions along one path of states before it considers any along an alternative path.
How does depth-first search (DFS) measure up?
The low cost of space in DFS is a result of only needing to store the path leading to a state, plus immediate siblings of each state on the path. The low cost of time in DFS is a result of the fact that in, most problems, solutions require a long sequence of actions--and DFS considers long sequences of actions sooner than BFS!
Let's step back for a second from the details of search to remind ourselves of what we've done. In order to plan ahead to find a solution, an intelligent agent goes through three distinct phases:
The result of "problem formulation" is a concrete definition of the problem:
Why does problem formulation follow goal formulation? Why does problem solution follow problem formulation?
We will not do much with goal formulation at this point. Why? In general, the problem is too hard. In narrow domains, we understand enough about goal formulation to incorporate it into our discussion. As you may imagine, much of what we consider intelligent behavior lies in formulating the 'right' goals!
Doing problem formulation for simple problems can't really capture the complexity of formulating problems in complex environments. Artificial tasks are fun, and a good way to start, but:
This leads to a sort of interleaving of deliberation and action that we often do when, say, solving a crossword puzzle. The puzzle doer needs to begin acting before it finishes reasoning, in order to use the information gained during the reasoning step.
The last step is where the agent actually searches for something. Search involves using an algorithm like the one we've been considering to explore the set of possible states, in search of a sequence of operations that leads from the initial state to a goal state.
Because search employs an algorithm, formulating a solution is objective: the algorithm defines the exact order in which states will be explored. This is different from problem formulation, which is subjective: there are multiple formulations for any problem that satisfy the definitions of our terms.
Random, breadth-first, and depth-first search strategies are considered uninformed because they do not use any knowledge about the problem being solved. The algorithm we've been considering works as well for finding a route between two cities as it does for solving a crossword puzzle, as well for scheduling experiments on the Hubble Space Telescope as it does for proving that a logical statement is true.
This generality is both a source of strength and of weakness:
How can an agent use knowledge of the world to do a better job solving problems?