I have code that processes a file of words and counts up how many start with each letter. For our old friend, the Unix dictionary, the result is this list:
The list "counts" contains the number of words by first letter:
[17096, 11070, 19901, 10896, 8736, 6860, 6861, 9027,
8799, 1642, 2281, 6284, 12616, 6780, 7849, 24461,
1152, 9671, 25162, 12966, 16387, 3440, 3944, 385,
671, 949]
The first item in the list is the 'a' words, the second item is the 'b' words, and so on, to the last item, which is the 'z' words. We need code that can look up the count for a particular letter.
Write a Python function look_up(letter, counts_list) that returns the count for the given letter.
For example:
>>> look_up('b', counts)
11070
>>> look_up('x', counts)
385
Then use your function to implement this interaction with the user:
Enter a letter: r
9671 of the words start with r.
That is 4.10% of all words.
How can we relate a letter to a specific integer relative to the other letters?
I can think of two ways:
>>> ord('a')
97
>>> ord('b')
98
>>> ord('z')
122
If we subtract ord('a') from each of these values, we will have an integer in the 0..25 range -- exactly what we need. So:
def look_up(ch, count_list):
index = ord(ch) - ord('a')
return count_list[index]
>>> alphabet = 'abcdefghijklmnopqrstuvwxyz'
>>> alphabet.find('a')
0
>>> alphabet.find('b')
1
>>> alphabet.find('z')
25
That gives us this solution:
def look_up(ch, count_list):
alphabet = 'abcdefghijklmnopqrstuvwxyz'
index = alphabet.find(letter)
return count_list[index]
(We can, of course, combine the first two lines.)
Here is my code. Can you think of any other to do this?
The techniques used in these two methods complement each other nicely. One uses computation on single values, while the other uses a data structure (a string) to simpolify the computation. You will learn about many such complements in your Data Structures course next semester.
Up until now, we have used two data structures: strings and lists. Each is a sequence: a collection of objects that appear in a particular order. Because the objects are in order, we can access them by their position, which is an integer. In many programming languages, the indexable sequence data structure is called an array.
We use the term index to refer to the position of an item in a string or a list. In Python code, we use a subscript that consists of square brackets and a number expression. For example, counts[i] accesses the ith item in counts, which can be a list or a string. In Python, we start counting positions with 0. (Have you figured out why yet?)
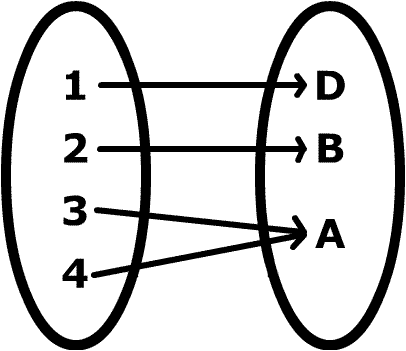
We can think of a sequence in another way. It is like a function that has a value for any position in some range of numbers. We programmers often think of functions as code that computes a value for us, but our mathematician friends ofthen think of a function as a relationship between two sets that maps an item in the domain set onto an item in the range set.

When we think of a list as a function, the domain is the set of integers from 0 to the length of the list (minus 1, of course). The range can contain values of any kind: numbers, strings, even other lists!
Sometimes, we want a data structure where the domain could be other kinds of objects, too. Consider our opening exercise. The main complication comes from the fact that we stored the count associated with 'a' in slot 0 of a list, and so on. It would have been handy if we could have created a data structure that mapped 'a' directly onto its count, 'b' directly onto its count, and so on.
|
|
Python gives us just such a data structure, the dictionary. A Python dictionary maps some maps objects of almost any kind -- not just integers, but also characters and string -- onto values of almost any kind. We can the items in a dictionary's domain its keys, and the items in the range its values.
This data structure is called a 'dictionary' as a metaphor based on the map with which most people are already most familiar: the book that maps words onto their meanings and derivations. Many other languages call this structure a dictionary, while others call it a map.
... convert the solution to our opening exercise to use a dictionary. We no longer need functions to find the position for a character or to look up the value associated with a character. The rest works much like the list-based solution...
... look at the example from last time. Similar.
... working with dictionaries.
... "out of order"? ... underneath, uses a hash function. Don't worry about the details!
... dictionaries are mutable. This is good for us, as it allows us to pass a dictionary to a function and have the function change its value. There is danger for us, too, as with lists: they hold references, which means they can share values.
Scores generally similar, but often a few points lower.
Extra credit opportunity. Open book. Use IDLE. Write up a new solution for any problem you missed points on. Worth up to 1/3 of the points you missed. (If over 50, not worth the points, but worth the study!)
The image of the function as a map comes from a question at the Mathematics Stack Exchange.
The image of the dictionary from Wikipedia. It is the icon for Mac OS X's Dictionary app.