 |
 |
 |
Suppose that we have this beginning of a binary tree in Java:
public class BinaryTree
{
private int value;
private BinaryTree leftTree;
private BinaryTree rightTree;
public BinaryTree( int nodeValue,
BinaryTree leftChild,
BinaryTree rightChild )
{
value = nodeValue;
leftTree = leftChild;
rightTree = rightChild;
}
}
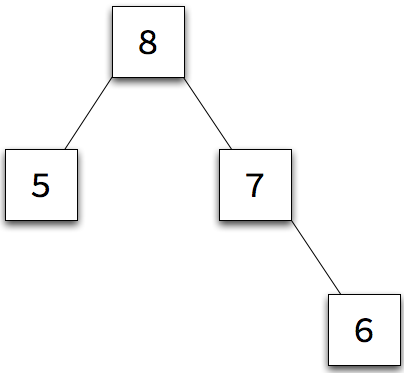
We could create the tree of one node (top left) with:
six = new BinaryTree( 6, null, null )
A node might have only one child (top middle):
seven = new BinaryTree( 7, null, six )
Here is a tree whose root has two children (top right):
eight = new BinaryTree( 8,
new BinaryTree( 5, null, null ),
seven )
 |
Fill in the blank:
public int nodeCount()
{
// the blank
}
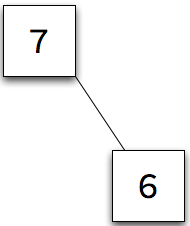
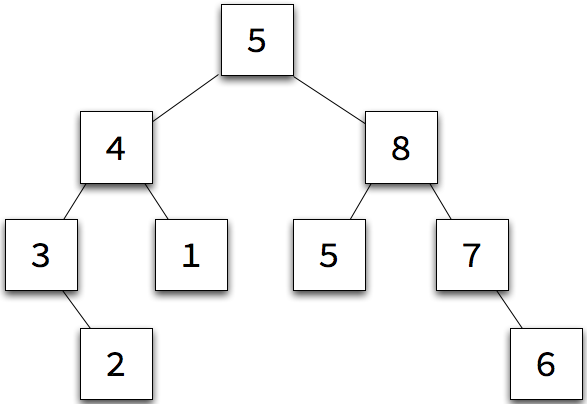
The tree at the right has a node count of nine.
If we try to think about this in terms of top-down control and a for loop, this can seem more difficult than it is. Instead, think about it in terms of the distributed control we see in the Cells of our Pousse game. Each tree contains its root node, plus all the nodes in its left subtree, plus all the nodes in its right subtree.
Consider the large example:
That sounds like an easy method to write:
public int nodeCount()
{
return 1 + leftTree.nodeCount() + rightTree.nodeCount();
}
Each subtree is smaller than the tree that contains it, so this method should terminate. But how?
When a tree does not have a left child (or right), the value of the instance variable is null. So we have to guard against these possibilities:
public int nodeCount()
{
if ( (leftTree == null) && (rightTree == null) )
return 1;
else if ( leftTree == null )
return 1 + rightTree.nodeCount();
else if ( rightTree == null )
return 1 + leftTree.nodeCount();
else
return 1 + leftTree.nodeCount() + rightTree.nodeCount();
}
This gives us a working solution.
This is a form of recursion that occurs often in an object-oriented program. When a BinaryTree receives a nodeCount() message, it responds by doing a computation that involves sending the same message -- nodeCount() -- to each of its instance variables, leftTree and rightTree.
The same message is sent, but to different objects. In an OO program, recursion is just a special case of what an object always does: send messages to its collaborators, so that they can do part of the job. We call this delegation: an object delegates some, even most, of the responsibility for responding to a message to its instance variables. Object recursion delegates using the same message.
Fill in this blank:
public int height()
{
// this blank
}
Our big sample tree has a height of 3. The subtree rooted at 7 has a height of 1.
...
One we know the pattern, writing code of this sort becomes straightforward. A tree is one taller than its taller child. Single-node trees have height 0. So:
if ( (leftTree == null) && (rightTree == null) )
return 0;
else if ( leftTree == null )
return 1 + rightTree.height();
else if ( rightTree == null )
return 1 + leftTree.height();
else
return 1 + Math.max( leftTree.height(), rightTree.height() );
And we have a working solution.
Now that we have written code like this twice, though, we realize that we probably aren't going to be satisfied with the result. The height() method repeats the control structure from nodeCount(). That makes the solution:
We have working solutions, but...
After eleven and a half weeks studying OO programming, can't we do better?
We can.
Object-oriented recursion is the right idea for solving this problem. However, writing the code naively means that we have to write a big if statement like the ones above for most of BinaryTree's methods. There are a lot of operations on a binary tree, so we will have to repeat this control structure a lot of times. They are all recursive, in just the same way.
How can we say it once and only once?
The usual way we say something only one is to factor the common behavior into a method and pass the part that changes as an argument. That doesn't seem to work here, because we need to pass four Java statements, one for each arm of the 2x2 if statement.
But in OOP, we have other ways to eliminate repeated code. They all revolve around different kinds of objects.
What is our big if statement really telling us? There are two kinds of tree: empty trees and non-empty trees.
Different kinds of tree behave differently. In response to a nodeCount() message,
Empty trees and non-empty trees also behave differently in reponse to a height() message, as well as most other messages we might send them. (Do you contain this value? Delete this value. What is the total value of your nodes?)
That sounds like two different objects.
Whenever you see a selection statement of the kind we wrote for BinaryTree, one that asks about the type or null-ness of an instance variable, ask yourself, "Does this code combine the responsibilities of two different objects?"
What distinguishes objects is how they behave.
What is the problem? Our use of null to terminate trees. In Java and most traditional languages, null is not an object and so cannot respond to messages.
Using null can be quite convenient:
left = new BinaryTree( 4,
new BinaryTree( 3,
null,
new BinaryTree( 2, null, null ) ),
new BinaryTree( 1, null, null ) );
... but that convenience comes at a cost. null is a "dead" data value. It does not respond to messages. As a result, our BinaryTrees must test for null cases and handle them differently from the usual case.
(Convenience always comes at a cost. Part of our job as designers is to weigh the costs and benefits for our program, and for the future of our program, and decide whether it is worth it.)
Keep in mind how simple the usual case often is... "A tree contains one more node than sum of the counts for its children." "A tree is one taller than its taller child." The only thing that made our code more complex was the need to test for null cases and handle them differently.
What is the solution? In object-oriented programming, the solution is often: a new kind of object.
We can use the idea of interchangeable objects to create different kinds of trees that have a common interface but different behaviors:
public interface BinaryTree
{
public int nodeCount();
public int height ();
}
Now, we write classes for both kinds of tree -- empty and non-empty -- that implement this interface. Notice how simple the methods in NonEmptyTree are... They look exactly like the one-line definitions we wrote when we didn't have to bother with null pointers!
Of course, we will have to change how we create binary trees in client code, too. Here is a new test client that replaces each occurrence of null with a new EmptyTree, and each occurrence of BinaryTree with a new NonEmptyTree. We pay for the better design of our tree objects with slightly less convenient client code.
But we can do better still. EmptyTrees don't have state -- no instance variables -- and always respond to the messages they receive in exactly the same way. That means we need only one EmptyTree, and it can serve as the terminator for all NonEmptyTrees. The resulting code is a bit simpler. In fact, it is quite similar to our original client, only with aLeaf used in place of null!
With only a little work, we can often regain the advantages of our original solutions in our new and improved solutions.
Now you try it:
public int max()
{
// the blank
}
Our big sample tree has a maximum of 8. The subtree rooted at 4 has a maximum of 4.
...
One we know this pattern, it too makes writing code of this sort relatively straightforward. The max in a tree is the largest of its value and the maximum values of its children. Empty trees have no maximum value.
What exactly does that mean? And what value must an EmptyTree return? [... discussion. Are the values in the tree only positive? Non-negative? Any integer? To allow the last of these, we need to return a value that is smaller than any int. The smallest is Integer.MIN_VALUE.
So:
public int max() { return Integer.MIN_VALUE; } // empty
public int max() // non-empty
{
int maxChild = Math.max( leftTree.max(), rightTree.max() );
return Math.max( value, maxChild );
}
We have a working solution. And it is pretty nice, if I do say so myself.
The technique we just used is a common one in OO programming.
The EmptyTree class is called a null object. A null object is an object that takes the place of null. Null objects are useful as terminators for dynamic data structures precisely because they support OO recursion without writing code for the special cases. They localize the special cases into a single object.
The null object pattern relies on the idea of interchangeable or substitutable objects. An EmptyTree can be used any place that expects a "real" binary tree. Generally, a null object is substitutable for the ordinary domain object, which allows us to implement methods and to write client code without worrying about what kind of object our instance variable holds.
This pattern takes advantage of two basic ideas of programming in this style:
...another example: cells in our Pousse game...
Keep the idea of substitutability in mind as you write Java programs. Over the next few weeks, we will consider several different problems we encounter when writing OO programs. Creating substitutable objects of various sorts will help us to solve these problems in elegant ways.
~~~~
The second pattern is object recursion. Like the null object, it solves a particular problem we run into while writing OO programs.
The Problem. We would like to add a behavior to an object that is built out of other objects, often the same kind of object.
Why Does This Problem Matter? Many responsibilities can only be carried out by an object looking at its parts. If we treat the instance variables as "atomic" units, we will have to write a lot of special-purpose code to handle the different cases, because null isn't an object.
The Solution. When a compound object receives the message, it sends the same message to its parts and then assembles its answer from the answers of its parts. When an atomic object receives the message, it constructs an answer from scratch and returns it.
Null objects and object recursion are patterns of computation that you will see over and over again in object-oriented programming. You will want to make them part of your programming toolbox, too.
Take a look at your solution to Homework 6. Study the methods and see how they embody the object recursion pattern. How could you use the null object pattern to eliminate all the null checks from your code?