We are given a set of 2n dots spaced evenly along a long line. n of the dots are blue, and n are red. The dots of each color are numbered 1..n.
The dots can appear in any order, with only one requirement. For any i in [1..n], the red-i dot appears to the left of the blue-i dot. For any other value of j in [1..n], though, the red-i and blue-i dots can appear left or right of the red-j and blue-j dots.
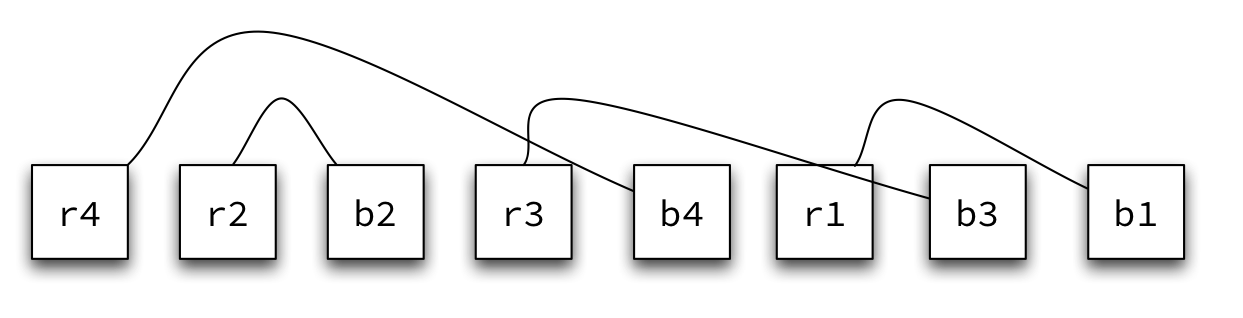
For example, this is a legal input:
r4 r2 b2 r3 b4 r1 b3 b1
Notice that every red dot is to the left of its corresponding blue dot, but otherwise we have a jumble.
Suppose that each red dot is connected to its corresponding blue dot.

We want to know the total length of the n connections along the straight line. For this configuration, the total is 4 + 1 + 3 + 2 = 10.
Your first task is this:
Write an algorithm to compute the total length of the connections for a given input.
Some candidate algorithms are O(n²). Can you achieve O(n)? Or better?
Next:
Generate a legal input with n = 5.
Try to make a challenging sequence, one that exploits the hardest part of the problem.
Finally:
Trade sequences with someone else. Apply your algorithm to the sequence you receive.
How well does your algorithm work?
What are some of the possible ways to attack this problem?
My first candidate uses brute force. I call it Single Array, Compute After:
INPUT: 2n values of form color:number
store the input in an array slots of size 2n
total ← 0
for i = 1 to n do
red_slot = slot of red-i
blue_slot = slot of blue-i
distance = blue_slot - red_slot
total = total + distance
return total
How well does Candidate 1 perform?
A variation of this approach creates two arrays, one for the color of the dot in position i, and one for the number on the dot. This behaves pretty much like the single array approach.
But once we strike upon the idea of multiple arrays, we can use it to create a better approach. Why not store the red dots in one array, and the blue dots in another? Then we can store their positions in the original input.
I call my second candidate Parallel Arrays, Compute After. It preprocesses the input.
INPUT: 2n values of form color:number
create two arrays of size n, red and blue
for each position in the input
store position in color[number]
total ← 0
for i = 1 to n do
distance = blue[i] - red[i]
total = total + distance
return total
How well does Candidate 2 perform?
Better! Can we do mo' better? Well, we know that we always see blue-i after red-i, so do we need to store the blue dots at all? We could compute the distance right then.
I call this candidate Single Array, Compute on the Fly. It store only the red dots.
INPUT: 2n values of form color:number
create one array of size n, red
total ← 0
for i = 1 to 2n do
if the dot is a red-j then
red[j] = i
else it is a blue-j
distance = i - red[j]
total = total + distance
return total
What improvements does Candidate 3 offer?
This improves in both space and time, but only in the constants. The complexity classes are the same. How can we do even better?
It sounds like we need a good invariant...
Notice that ...
Σ [ position(blue-i) - position(red-i) ]
... is equal to ...
[ Σ position(blue-i) ] - [ Σ position(red-i) ]
So we don't need to store any dots at all! I call the algorithm that takes advantage of this little trick One Good Invariant. It store no dots.
INPUT: 2n values of form color:number
total ← 0
for i = 1 to 2n do
if the dot is a red-j then
total = total - i
else it is a blue-j
total = total + i
return total
Now we see an improvement in the order of the algorithm:
Nice.
This is about as far as most of us would go with this problem. We have a solution that is O(1) in space and O(n) in time. But a few creative computer scientists have come up with a variant of One Good Invariant that can often be implemented slightly more efficiently. It frames the algorithm in terms of the differences rather than the positions.
We might call this version Explicit Delta.
INPUT: 2n values of form color:number
delta ← 0
total ← 0
for i = 1 to 2n do
if the dot is red then
delta = delta + 1
else it is blue
delta = delta - 1
total = total + delta
return total
This algorithm uses two counters, one for the delta and one for the running total, independent of n. This is still O(1) in space. It still makes a single pass over 2n items, which is O(n) in time. But the arithmetic may well be simpler, shaving off some of the constant overhead cost of the computation.
You may well look at this algorithm and say,
That can't possibly work. I don't believe you.
Fair enough. I didn't quite believe it myself. So do what I did.
Quick Exercise: Trace the Explicit Delta algorithm on our example input above:
r4 r2 b2 r3 b4 r1 b3 b1
Trust me. I won't lead you astray...
The last two algorithms above may seem a bit clever for us to create on our own. But they use a common idea that computer scientists have re-discovered in many domains. It's an idea that, once we know about it, we can use to solve many sequence processing problems efficiently.
Context
- We are counting the differences between values of complementary 'types'.
Forces
- If there are multiple complementary values, then we might process each value separately. But then we have to process the list multiple times for each of the values. That's O(n²) in time.
- If we store "history" information as we process the list, in order to iterate through it only once, then we need O(n) space to accumulate information for each value.
- The differences are more important than the actual values or the absolute counts.
Solution
- Maintain a counter that records the difference among items.
- Increment or decrement the counter on each input.
- If you are summing over multiple pairs, use the counter to update the running sums.
This is called the Sliding Delta pattern. The counter maintains the delta.
Examples
- A really simple example of using a sliding delta is for determining the winner of a two-person election.
If we care only about knowing who the winner is, not the final vote counts, we can use a sliding delta. If we know the size of the input, we can even recover the vote tallies from the delta. This requires O(n) time and minimal O(1) space.
- Dot connections is another example. This problem is an abstraction of many circuit layout and design problems. We need to know the deltas between all pairs, which we accumulate into an overall tally. For such a problem, we can use the delta at each blue dot to update another counter that is the running sum.
- Another example: sliding windows in communication protocols. Some of you may have seen this in your Networking course.
Mathematical Basis
- After processing the kth item, the delta records the "balance" accumulated through the first k values. As a relative value, it eliminates the need for absolute positions or counts for each item.
Mathematical Characteristics
- O(1) in space
- O(n) in time
Whenever you encounter a problem that fits the profile of a sliding delta, this pattern can be handy.
We are given a sequence of n parentheses, left and right, in any order.
For example, (( is a legal sequence. So is ()). As are ((())) and ((())))(()())((()).
An onion is a subsequence of 2k parentheses where the first k are left parentheses and the second k are right parentheses, (((...))). Notice that, when k > 1, the onion contains smaller onions.
We are interested in the number of onions in the input.
For the examples above, the number of onions are 0, 1, 3, and 7, respectively.
Write an algorithm to compute the number of onions in a given input.
Doing this in O(n) space isn't too difficult. Can you do it in O(1)?
The first idea to come to mind is one you may have encountered when studying data structures. It uses a stack.
stack ← empty
total ← 0
while there is input do
if input is ( then
push stack
else if stack not empty
pop stack
total ← total + 1
return total
The worst-case scenario for this algorithm is a large input of size n = 2k, consisting of k left parentheses followed by k right parentheses. In this case, we store k items on the stack, and space usage is O(n).
There's a subtle difficulty lying in this approach. How can we ensure that (()()) counts as only two onions, not three? The outer pair of parentheses is not an onion! But the stack loses context, and we get the wrong answer
Perhaps we can fix the stack-based algorithm to make it work. But there is a simpler candidate 2, based on the Sliding Delta pattern.
This is O(n) in time, of course, but uses minimal space -- only two counters and one character for the input.
What, again you don't believe me? That's fine. Trace this algorithm on all four examples above. Does it work?
Identify another "algorithmic pattern" from our previous study this semester: a common idea that, like sliding delta, cuts across multiple types of problems and appears in different algorithms -- even if in a different form.