It is time for an annual business summit, and feuds among the CEOs threaten to ruin the fun. Your reputation for helping circumvent relationship problems earns you another client.
Summit organizers have invited n CEOs to the meeting. They have rented a big, round table for discussion. Unfortunately, many of the guests do not get along with one another. Every dislike is mutual, and some guests dislike a lot of other guests, having up to ½n-1 enemies in the group.
You are given as input a file of n lines. Each line consists of a guest's name followed by a list that guest's enemies. For example:
G1 G3 G5
G2 G4 G5
G3 G1
G4 G2
G5 G1 G2

|
Your task is this:
Design an algorithm that creates a seating arrangement in which no person sits next to an enemy.
The output of your algorithm can be a list beginning at any seat of the table, for example:
G1 G2 G3 G5 G4
I'll offer the same suggestion as last time: Draw pictures.
What options do we have?
Brute force is especially unappealing on this problem. We could consider all possible seating arrangements, but that requires examining every permutation of n items. Ouch.
A group of students once proposed this algorithm in class:
seating = empty list
guests = queue containing all guests
until guests is empty
g = guests.dequeue()
if g will sit by rightmost guest in seating,
seat g there
else if g will sit by leftmost guest in seating,
seat g there
else
guests.enqueue(g)
What is the complexity of this algorithm? O(n). That sounds good. But does it work? Sadly, no. It could fall into infinite loop, dequeuing and re-queuing the same guests. (Can you find an example?)
This algorithm can also get into a state that it can't resolve. Suppose that algorithm starts with a guest list of:
G3 G4 G5 G1 G2
It would place G3, then G4 to the right, G5 to the right. G1 can't sit next to either G3 or G5, so it goes back into the queue. It places G2 on the left. Now, only G1 remains. It can't sit next to G5, so the algorithm places it on the left, resulting in:
G1 G2 G3 G4 G5
But we have one last check to make: are the guests on the ends willing to sit next to one another? We have G1 seated next to G5, and causes the summit to crash.
To resolve this problem, the algorithm needs to backtrack: to return to some earlier decision, and try another alternative. But that can be very expensive time-wise, as well as requiring that we keep record of past decisions.
|
Is there any way to rehabilitate this algorithm?
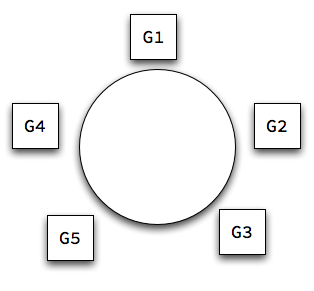
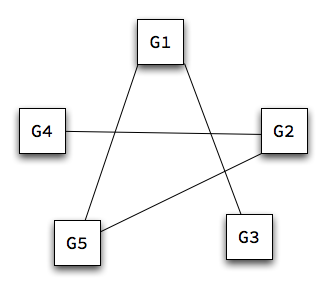
One feasible approach is to transform the problem into a graph problem. We can interpret our input as depicting the graph in the picture to the right. Each guest is a node, and an edge indicates that two guests are enemies.
Our task, though, is to find a seating chart that avoids pairing enemies, so we are actually more interested in the graph of friend relationships. What we need is the complement of this graph, in which an edge indicates that two guests are willing to sit next to one another:
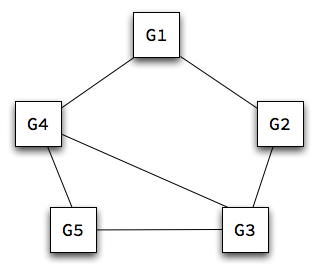
Notice that there is now an edge wherever there wasn't an edge before.
Transforming our data representation in this way transforms the problem, too. Our task is now to find a cycle in the friends graph that contains all n nodes. Visually, this task is quite easy. It's obvious that the arrangement given as an example above is the only seating that works for our guests. But how can algorithm find it?
Finding cycles in a graph is one of the classic sets of combinatorial problems in computer science. Indeed, most people date the beginning of graph theory to Leonhard Euler's paper on Seven Bridges of Königsberg, in which he solved a slightly different problem: trying to find a cycle in a particular graph that contained all n edges.
A cycle that contains every vertex exactly once is called Hamiltonian cycle. In the general case, finding a Hamiltonian cycle in a graph is exponential. But our problem is a special case: no guest has as many as ½n enemies. In this case, there is a "clever iteration based on an illuminating invariant property". Can you find it?
In the reading left for you in last session's notes, you considered the problem of finding a pair with a given sum in an array of integers. We considered two algorithms:
Last semester, a student suggested yet another algorithm, using a binary search tree or a hash table:
INPUT: A, an array of integers
sum, a target sum
aux ← empty binary search tree or hash table
for each item a in A
if aux contains a
then return true
else insert (sum - a) into au
This algorithm makes a single pass through the array, inserting the difference between sum and A[i] into the auxiliary structure. That way, if a future look-up succeeds, then we were looking up the matching value for an earlier array item.
If we use an O(log n)-lookup data structure, then our algorithm is O(n log n). If we use an O(1)-lookup data structure, then our algorithm is O(n)!
Code for simple implementations of all three algorithms is included in today's zip file. Feel free to play around with it!
You are given a handful of uncooked spaghetti. The box was dropped, and the noodles are of varying lengths.
Your task: Write the spaghetti sort algorithm, which returns the noodles in descending order of length.
Your second task: Explain why the professor asked such a silly question today.
I do this all the time:
Like our pancakes, this problem uses analog data in place of a numerical representation. That gives us a visual way both to understand the problem and to design a solution.
We might consider this algorithm an example of a representation change. We presorted!
There is another reason I use this example today. The principle used is the same as that of the heap data structure, to which we turn our attention next. And, like the use of a hashtable in an algorithm for pairwise sums, using a heap can often make some problems seem much easier to solve.
An outline of what we discussed
... next time, more! Details and use, including for sorting.