TITLE: More Fun with Integer "Assembly Language": Brute-Forcing a Function Minimum
AUTHOR: Eugene Wallingford
DATE: December 16, 2013 2:20 PM
DESC:
-----
BODY:
Or: Irrational Exuberance When Programming
My wife and daughter laughed at me yesterday.
A few years ago, I blogged about
implementing Farey sequences
in Klein, a language for which my students at the time were
writing a compiler. Klein was a minimal functional language
with few control structures, few data types, and few built-in
operations. Computing rational approximations using Farey's
algorithm was a challenge in Klein that I likened to "integer
assembly programming".
I clearly had a lot of fun with that challenge, especially
when I had the chance to watch my program run using my students'
compilers.
This semester, I am again teaching the compiler course, and
my students are writing a compiler for a new version of Klein.
Last week, while helping my daughter with a little calculus,
I ran across a fun new problem to solve in Klein:
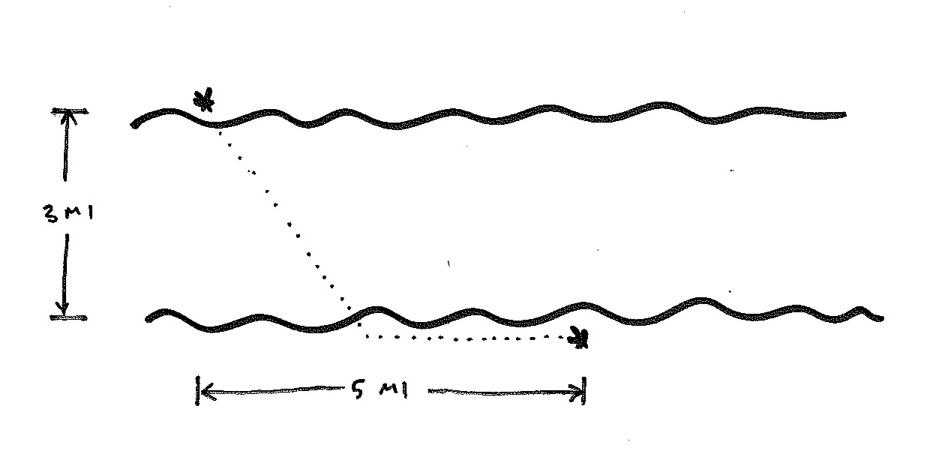 There are two stations on opposite sides of a river. The
river is 3 miles wide, and the stations are 5 miles apart
along the river. We need to lay pipe between the stations.
Pipe laid on land costs $2.00/foot, and pipe laid across the
river costs $4.00/foot. What is the minimum cost of the
project?
This is the sort of optimization problem one often encounters
in calculus textbooks. The student gets to construct a couple
of functions, differentiate one, and find a maximum or minimum
by setting f' to 0 and solving.
Solving this problem in Klein creates some of challenges.
Among them are that ideally it involves real numbers, which
Klein doesn't support, and that it requires a square root
function, which Klein doesn't have. But these obstacles are
surmountable. We already have tools for computing roots
using
Newton's method
in our collection of test programs. Over a 3mi-by-5mi grid,
an epsilon of a few feet approximates square roots reasonably
well.
My daughter's task was to use the derivative of the cost
function but, after talking about the problem with her, I was
interested more in "visualizing" the curve to see how the cost
drops as one moves in from either end and eventually bottoms
out for a particular length of pipe on land.
So I wrote
a Klein program
that "brute-forces" the minimum. It loops over all possible
values in feet for land pipe and compares the cost at each
value to the previous value. It's easy to fake such a loop
with a recursive function call.
The programmer's challenge in writing this program is that
Klein has no local variables other function parameters. So
I had to use helper functions to simulate
caching temporary variables.
This allowed me to give a name to a value, which makes the
code more readable, but most importantly it allowed me to
avoid having to recompute expensive values in what was already
a computationally-expensive program.
This approach creates another, even bigger challenge for my
students, the compiler writers. My Klein program is naturally
tail recursive, but tail call elimination was left as an
optional optimization in our class project. With activation
records for all the tail calls stored on the stack, a compiler
has to use a lot of space for its run-time memory --
far more than is available on our default target machine.
How many frames do we need? Well, we need to compute the cost
at every foot along a (5 miles x 5280 feet/mile) rectangle, for
a total of 26,400 data points. There will, of course, be other
activation records while computing the last value in the loop.
Will I be able to see the answer generated by my program using
my students' compilers? Only if one or more of the teams
optimized tail calls away. We'll see soon enough.
So, I spent an hour or so writing Klein code and tinkering with
it yesterday afternoon. I was so excited by the time I finished
that I ran upstairs to tell my wife and daughter all about it:
my excitement at having written the code, and the challenge it
sets for my students' compilers, and how we could compute
reasonable approximations of square roots of large integers even
without real numbers, and how I implemented Newton's method in
lieu of a sqrt, and...
That's when my wife and daughter laughed at me.
That's okay. I am programmer. I am still excited, and I'd do
it again.
-----
There are two stations on opposite sides of a river. The
river is 3 miles wide, and the stations are 5 miles apart
along the river. We need to lay pipe between the stations.
Pipe laid on land costs $2.00/foot, and pipe laid across the
river costs $4.00/foot. What is the minimum cost of the
project?
This is the sort of optimization problem one often encounters
in calculus textbooks. The student gets to construct a couple
of functions, differentiate one, and find a maximum or minimum
by setting f' to 0 and solving.
Solving this problem in Klein creates some of challenges.
Among them are that ideally it involves real numbers, which
Klein doesn't support, and that it requires a square root
function, which Klein doesn't have. But these obstacles are
surmountable. We already have tools for computing roots
using
Newton's method
in our collection of test programs. Over a 3mi-by-5mi grid,
an epsilon of a few feet approximates square roots reasonably
well.
My daughter's task was to use the derivative of the cost
function but, after talking about the problem with her, I was
interested more in "visualizing" the curve to see how the cost
drops as one moves in from either end and eventually bottoms
out for a particular length of pipe on land.
So I wrote
a Klein program
that "brute-forces" the minimum. It loops over all possible
values in feet for land pipe and compares the cost at each
value to the previous value. It's easy to fake such a loop
with a recursive function call.
The programmer's challenge in writing this program is that
Klein has no local variables other function parameters. So
I had to use helper functions to simulate
caching temporary variables.
This allowed me to give a name to a value, which makes the
code more readable, but most importantly it allowed me to
avoid having to recompute expensive values in what was already
a computationally-expensive program.
This approach creates another, even bigger challenge for my
students, the compiler writers. My Klein program is naturally
tail recursive, but tail call elimination was left as an
optional optimization in our class project. With activation
records for all the tail calls stored on the stack, a compiler
has to use a lot of space for its run-time memory --
far more than is available on our default target machine.
How many frames do we need? Well, we need to compute the cost
at every foot along a (5 miles x 5280 feet/mile) rectangle, for
a total of 26,400 data points. There will, of course, be other
activation records while computing the last value in the loop.
Will I be able to see the answer generated by my program using
my students' compilers? Only if one or more of the teams
optimized tail calls away. We'll see soon enough.
So, I spent an hour or so writing Klein code and tinkering with
it yesterday afternoon. I was so excited by the time I finished
that I ran upstairs to tell my wife and daughter all about it:
my excitement at having written the code, and the challenge it
sets for my students' compilers, and how we could compute
reasonable approximations of square roots of large integers even
without real numbers, and how I implemented Newton's method in
lieu of a sqrt, and...
That's when my wife and daughter laughed at me.
That's okay. I am programmer. I am still excited, and I'd do
it again.
-----

