Homework Assignment 6

General Algorithm Design Techniques

CS 3530
Design and Analysis of Algorithms
Spring Semester 2014

Due: Friday, May 2, at 5:00 PM

Notes

Problems 1 and 3 ask you to write code. Problems 2 and 4 are pencil-and-paper exercises.

The programming problems are smaller than the ones we've done on other homework assignments, but I'd still follow the basic advice from Homework 5: Start small. Take small steps. It is okay to implement something that is quick and dirty and guide it into something that is cleaner and more efficient.

Tasks

1. Implement the dynamic programming algorithm for the World Series problem as a function or object in a programming language of your choice. Then use your code to compute P(3,5) when p = 0.25. (Note that Team 2 needs to win five games yet, so this must be at least a nine-game series.)

   Extra credit. Make it so that not only the size of the grid and the value of p can be passed in, but also the rules for filling in the grid. Demonstrate that your extension works on an example of your own choice.



2. Show that the dynamic programming approach to the Knapsack Problem, described in Session 28 and its assigned reading, is O(nW) in time. You may find it helpful to sketch the algorithm in greater detail first.



3. Consider this scheduling problem... We have a single processor on which to run n jobs of lengths t₁, t₂, ... t_n. We can execute the jobs in any order we like. We want a schedule that minimizes total time spent in the system by all jobs. The time spent in the system by job k is the time it spends waiting to start plus the time it spends running.

   One greedy approach to solving this problem is to execute the longest jobs first and the shortest jobs last. We'd like to know how well this approach performs in practice. So...

   Implement this approach as a function or object in a programming language of your choice. Demonstrate its performance on at least ten random inputs where n ≥ 100. Show the results in a table.

   Extra credit. Write a formal proof that the greedy approach is or is not optimal. You may want to consider some examples for small values of n and generalize what you learn from them.



4. Use Dijkstra's Algorithm from Session 29, to find the shortest paths from vertex c to all other vertices in the following graph:
   

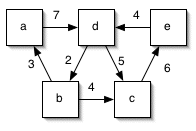
Create a readme.txt file that presents:

• anything I need to know to compile and run your programs for Problems 1 and 3
• a table summarizing the results of your experiments for each

Deliverables

By the due time and date, submit

• a zipped archive named homework06 containing:
  • your readme.txt file
  • all of your source files
• hardcopy of your readme.txt and solutions to Problems 2 and 4

Be sure that your submission follows all homework submission requirements.