CS 3540: Programming Languages and Paradigms

Using Syntax Procedures for Complex Data

We encounter a certain kind of problem in all sorts of programming, because programming deals with data abstraction. The problem takes on even more meaning when we are writing especially complex code, of the sort we write when doing recursion on a complex data type.

Very often, when programming, we use a data structure from our programming language to implement an "abstract" data type, that is, a data type not defined as primitive in our language. For example, we might use a Racket list to implement a set data type. (In fact, you may do this for a future homework assignment.)

But when we write client code that uses sets, any references to the underlying implementation have at least two negative effects. First, any change to the data implementation requires a change to the client code. You studied this problem in some detail in your Data Structures and will see it again in Intermediate Computing.

Second, the code you write does not look like it is operating on the abstract type; it looks like it is operating on the underlying implementation! The use of built-in functions such as car and vector-ref distract the reader from the set operations, requiring constant translation in the reader's mind. This second problem is an intensely human problem, one that affects the programmer and reader alike. Why should I have to translate one set of operations into another in my head? Why doesn't the program say what it means?

In a language such as Java, the typical solution is to create a class that encapsulates the implementation. This class provides a public interface that specifies the operations on the data type. Then, if the implementation changes, clients are protected, since they refer only to the public interface.

In functional programming, we solve both problems by using syntax procedures.

Example 1: A Point Data Type

Consider the simple example of a point data type. If we decide to represent points as (x . y) pairs, then we might implement a function to compute the distance between two points as follows:

(define distance
    (lambda (x y)
      (sqrt (+ (square (- (car x)
                          (car y)))
               (square (- (cdr x)
                          (cdr y)))))  ))

I don't know about you, but I find this code confusing on two levels.

• First, x and y are points, each of which have an x-coordinate and y-coordinate. So (cdr x) means the y-coordinate of the first point. x and y are not very good names for those parameters. When using a programming language without explicit data types for names, we should use names that reveal information about the expected types of their values. Many folks call this the type-revealing names pattern.
• Second, (car x) and (cdr x) mean "x-coordinate" and "y-coordinate". Why doesn't our code say so? And what happens if we decide to implement points differently, say, as two-place vectors?

That's why most programmers prefer a distance function that works like this:

(define point->x car)
(define point->y cdr)

(define distance
    (lambda (point1 point2)
      (sqrt (+ (square (- (point->x point1)
                          (point->x point2)))
               (square (- (point->y point1)
                          (point->y point2))))) ))

That code says what we mean.

Example 2: A Binary Tree Data Type

Now consider the following example dealing with binary search trees. The BNF definition for our binary search tree data type is:

<bst> ::= ()
        | (<number> <bst> <bst>)

In the second arm of this definition, the first <bst> refers to the left child, and the second refers to the right child. For example, the following expression:

'(14 (7 () (12 () ()))
     (26 (20 (17 () ())
             ())
         (31 () ())))

corresponds to the tree shown in the following diagram:

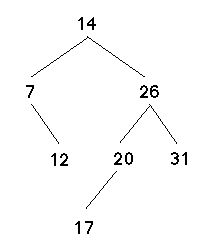
Let's write a function (path n bst) that returns a list of directions (either 'left' or 'right') for finding the number n in a binary search tree of numbers, bst.

Following the data definition, a BST is either an empty tree or a triple of node label, left subtree, and right subtree. So we write:

(define path
  (lambda (n bst)
    (if (null? bst)
        ...                 ;; we didn't find n
        ...                 ;; is this the right node?
        )))

If we ever get to an empty tree, then the number we were looking for wasn't in the tree, so we'll signal an error using Racket's built-in error function:

(define path
  (lambda (n bst)
    (if (null? bst)
        (error 'path "number not found!")
        ...                           ;; is this the right node?
        )))

When bst is not an an empty tree, we're at a node and there are possible three cases:

1. The number were looking for is less than this node.
2. The number were looking for is greater than this node.
3. The number were looking for is at this node.

So the code becomes:

(define path
  (lambda (n bst)
    (if (null? bst)
        (error "path: number not found!")
        (if (< n (first bst))
            ;; n is in the left subtree
            (if (> n (first bst))
                ;; n is in the right subtree
                ;; n is here!
            )))))

Now, we build the path by consing the correct directional letter into the solution return by searching the corresponding subtree, or just return the empty list if the node is here:

(define path
  (lambda (n bst)
    (if (null? bst)
        (error "path: number not found!")
        (if (< n (first bst))
            (cons 'left (path n (second bst)))
            (if (> n (first bst))
                (cons 'right (path n (third bst)))
                '() )))))

The result is a working solution. But look at it! With the use of first, second, third, and null?s, we can't see the tree for the forest of code. All of the thinking that went into the solution has been translated away into implementation details. And if we decide to change our tree representation from lists to, say, vectors later, we will have a lot of work to do to bring path up to spec.

Suppose that, before we began to write path, we had first defined several syntax procedures to access elements on our BNF definition. These functions should allow us to write path using the language of binary search trees, not the underlying Racket definitions of these terms. One of the nice things about Racket's flexible abstraction mechanism is that we can always use names that match our problem and not Racket's vocabulary, if we want!

Here are the syntax procedures we would want:

(define empty-tree?   null?)
(define node-value    first)
(define left-subtree  second)
(define right-subtree third)

Notice, that, since our tree language operations can be mapped directly onto Racket primitives, we can take advantage of Racket's function-naming features to create new, more meaningful names quite easily!

We can now run through the same development process for path, based on the BNF definition, but using the syntax procedures to operate on the parameter bst. The result is:

(define path
  (lambda (n bst)
    (cond ((empty-tree? bst)
              (error "path: number not found!"))
          ((< n (node-value bst))
              (cons 'left (path n (left-subtree bst))))
          ((> n (node-value bst))
              (cons 'right (path n (right-subtree bst))))
          (else             ;; we are sitting on it!
              '()))))

Notice:

• It was pretty easy to write the syntax procedures.
• Using the syntax procedures did not make writing path any more difficult; it was probably easier since we no longer had to think about how trees were implemented. We could think — and code — in the language of trees.
• The resulting function is easier to read.
• If we later change the data representation of trees, the change will not affect the definition of path, only the syntax procedures.

You will occasionally here me say, Speak the language! When writing programs, we should speak the language of our application domain. The result is code that is easier to write, easier to read, and easier to modify.

Further Study

You can download the code for this reading as a zip file. It contains one file with the first version of path and another file with the version that uses syntax procedures.