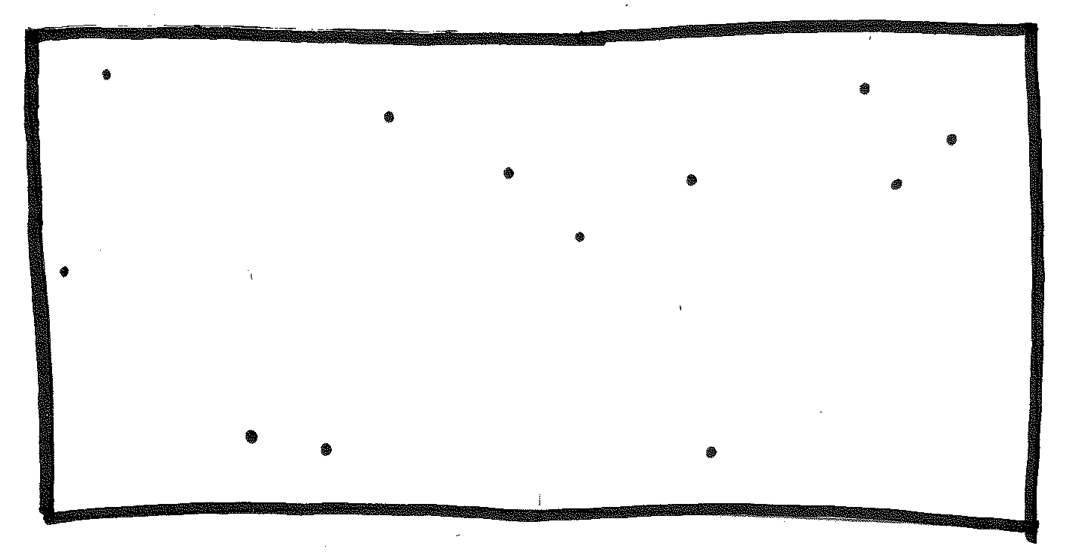
This is a classic problem called Closest Pair. We have a set of points in a rectangle. For example:

Let's label the points p1, p2, ..., pn, where each pi is an ordered pair (xi, yi).
Your task: Design an algorithm that finds the closest pair of points.
Recall that the distance formula for two points in a plane is:
sqrt( (x2 - x1)2 + (y2 - y1)2 )
How efficient is your solution?
We could do this in a brute force manner by computing the distance between every pair of points and selecting the smallest:
INPUT: x[1..n] and y[1..n]
minimum ← ∞
for i ← 1 to n do
for j ← i+1 to n do
distance ← sqrt((x[i] - x[j])² + (y[i] - y[j])²)
if distance < minimum then
minimum ← distance
first ← i
second ← j
return (first, second)
What is the complexity of this algorithm? O(n²), because we have to do (n**2-n)/2 distance computations. These are very expensive due to the square root operation. One way to improve the algorithm's performance is not to compute the square root! If sqrt(x) < sqrt(y), then x < y. If we really need the distance of the closest pair, we can compute it once we know first and second. Still, though, the algorithm is O(n²).
Let's try a top-down approach: divide and conquer. Split the grid in half. Solve the two halves, finding the closest pair on the left and the closest pair on the right. Choose the smaller of the two.
We don't need to go all the way. If a panel has k points or fewer, then we can solve it with the brute-force approach. For small enough k, O(k²) is acceptable. If not, though, divide and conquer. Let's use k = 3, as that means we don't need a nested loop...
With this algorithm, we end up with four smaller rectangles:
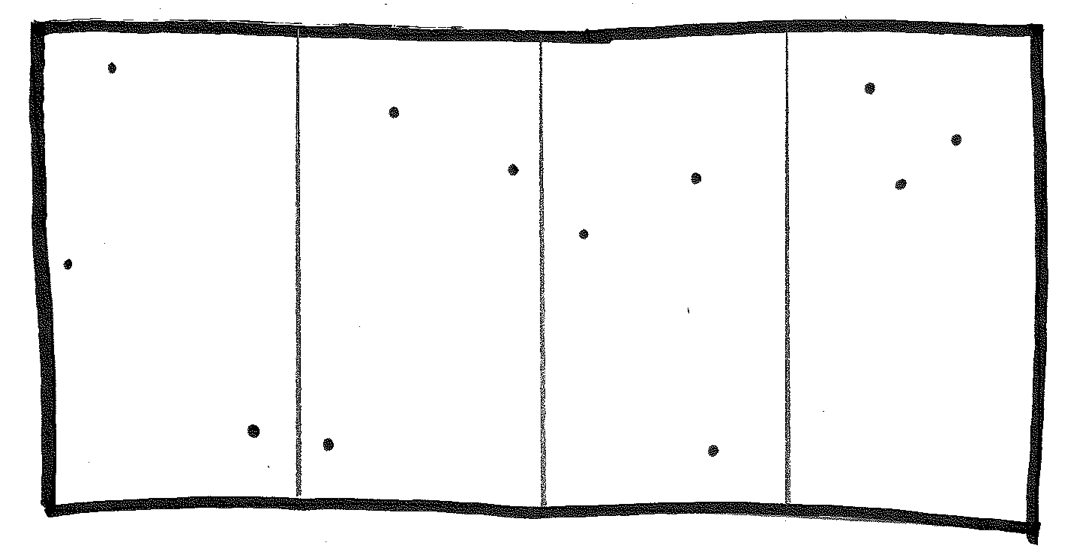
Solve left half, as two panels of size three. This gives us two pairs, separated by dleft and dright, respectively. Choose the smaller, dmin.
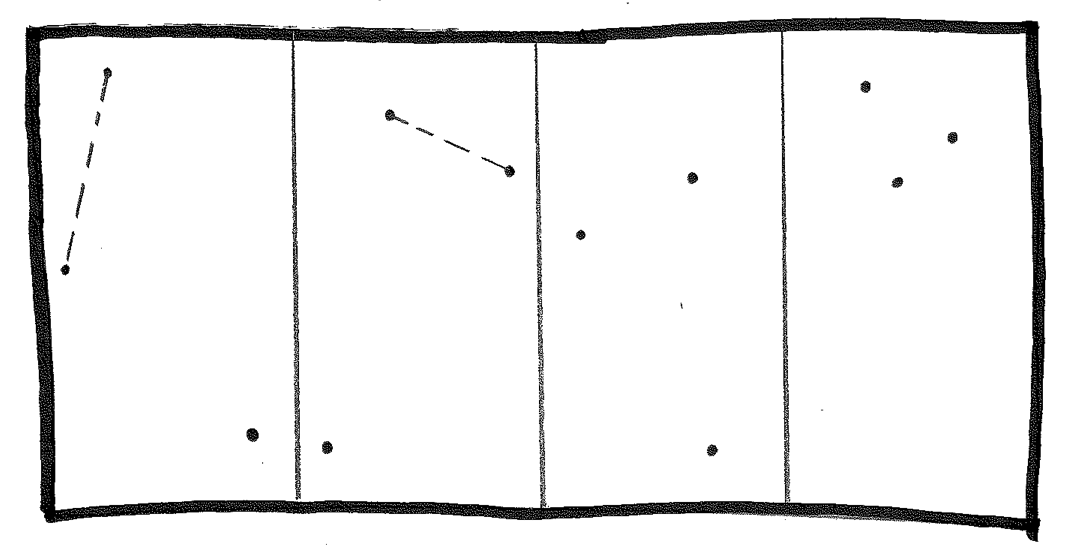
Complication... The closest pair in the left rectangle might not be within one of the halves -- it could straddle the dividing line! Let's consider all the possibilities. But we can narrow our search... How close would straddling points have to be to the dividing line in order to be closer to each other than our closest pair in each half? dmin.
Find the closest pair in the straddling region. (Use the same algorithm!!). In this case, a straddling pair is the closest pair, so choose it as the answer for the left half.
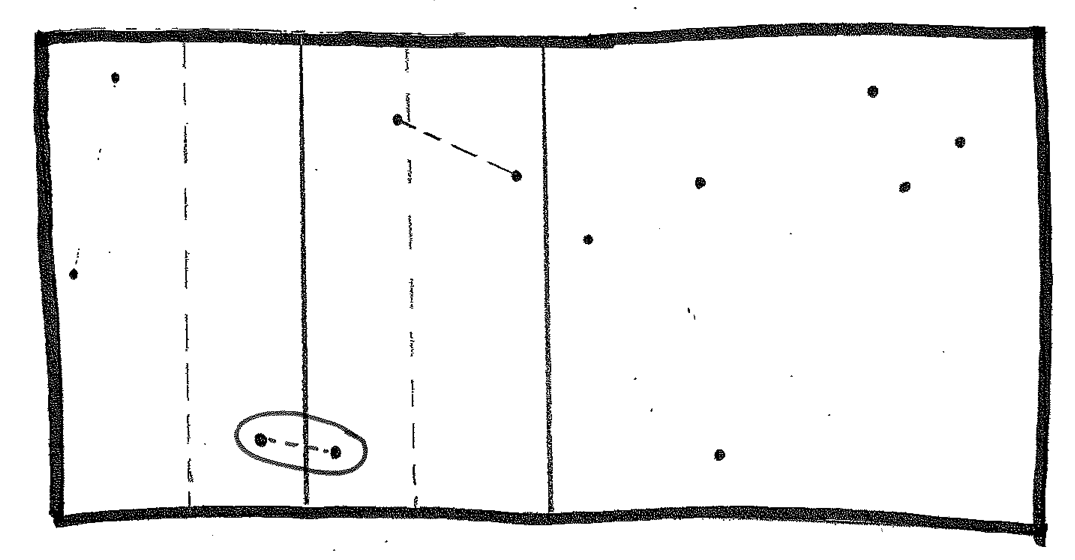
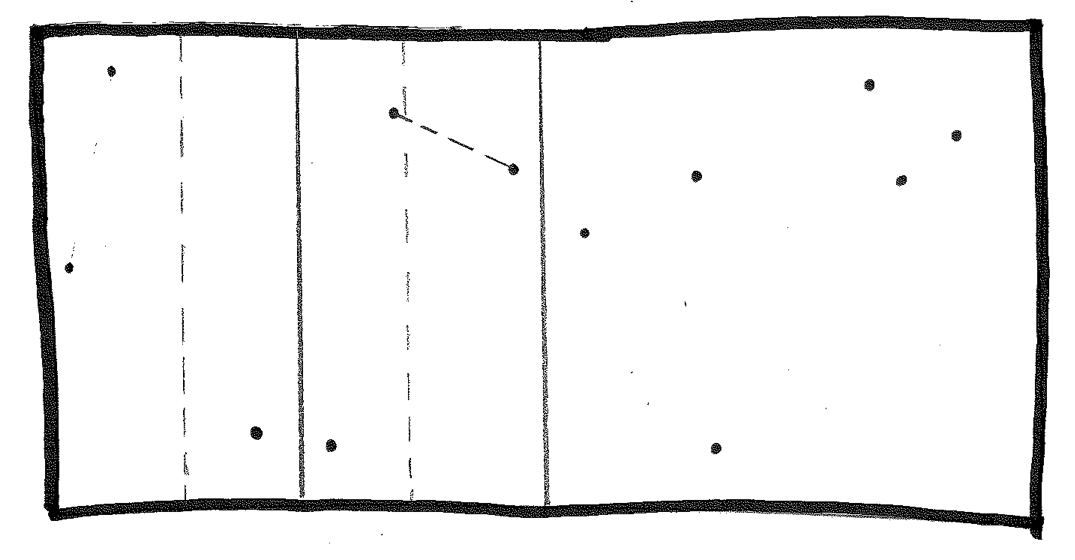
Now, solve the right half, including its sanity check. That gives us two points:
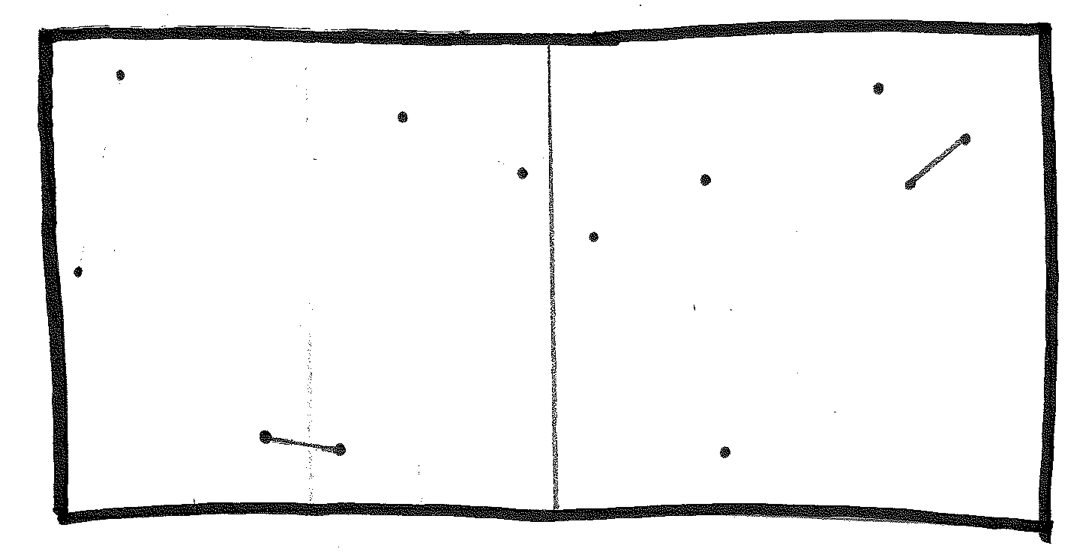
Then combine left and right, with its sanity check, and we have the closest pair in the original set.
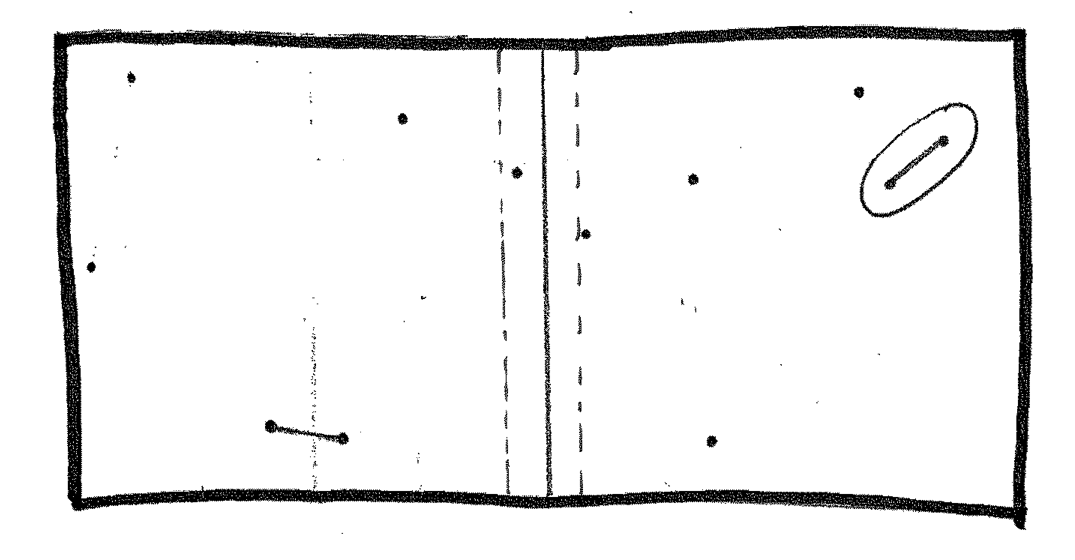
How efficient is this approach?
T(1) = c c == min(three computed distance)
T(n) = 2T(n/2) + B B == cost to combine the two halves
The cost of combining the two halves is the cost of checking the straddling region. This is Θ(n). (Can you figure out why?)
The overall complexity is Θ(n log n), which improves on our brute-force solution. ... in much the same way that quicksort and mergesort improve on the O(n²) sorts!
Brute-force is often a good way to start looking for an algorithm, if only to create a baseline for how good we can do. Then we can proceed as we learned the first couple of weeks, with top-down and bottom-up, always being on the look-out for a useful invariant or bit of knowledge that might let us zoom-in.
We can learn an interesting lesson here. Divide-and-conquer doesn't work here, strictly speaking. But "we made it fit" by accounting for the way it fails. The lesson... Use the basic techniques. Tweak as necessary.
Last time we began formally analyzed an iterative algorithm and then started to analyze a recursive algorithm before reaching the end of our time. Let's pick up where we were.
Our Algorithm Q(n) computes the sum of the first n cubes. Its basic operation is the double multiplication done on each call.
if n = 1
then return 1
else return Q(n-1) + n * n * n
First, we set up a recurrence relation for the number of multiplications:
M(1) = 0
M(n) = M(n-1) + 2
Then, we started to substitute previous values for M into the equation unntil we saw a pattern for n-i:
M(1) = 0
M(n) = M(n-1) + 2
= (M(n-2) + 2) + 2 = M(n-2) + 4
= (M(n-3) + 2) + 4 = M(n-3) + 6
= (M(n-4) + 2) + 6 = M(n-4) + 8
...
... = M(n-i) + 2i
Once we have that, we can substitute n−1 for i to reach a solution for the problem of size n in terms of a problem of size 1. We know the cost of that problem, so we can simplify down to a value in terms of n itself.
M(1) = 0
M(n) = = M(n-i) + 2i
...
[substitute i = n-1] = M(n-(n-1)) + 2(n-1)
= M(1) + 2(n-1)
= 0 + 2(n-1)
= 2(n-1)
So this algorithm performs 2(n-1) multiplications and is O(n).
When analyzing any recursive algorithm, we can use this same process:
Often, the arithmetic for solving a recurrence relation is simpler than that needed to solve the iterative sum. Loops may seem easier to understand than recursion, at least until you gain more experience, but recursion is often much better behaved mathematically!
Show Towers of Hanoi: interactive!
Algorithm:
Analyze this.
Apply the technique...
M(1) = 1
M(n) = = 2*M(n-1) + 1
= 2*(2*M(n-2) + 1) + 1 = 4*M(n-2) + 3
= 4*(2*M(n-3) + 1) + 3 = 8*M(n-3) + 7
...
= ... = 2iM(n-i) + (2i-1)
...
[substitute i = n-1] = 2n-1M(1) + (2n-1-1)
= 2n-1 + 2n-1 - 1
= 2n - 1
Quick question. What would it mean to startg with M(0)? Would that work?
So, this algorithm is O(2n). That is much worse than O(n2), even O(nk) for k > 2. Check out this chart I found via a University of Ottawa CS course site:
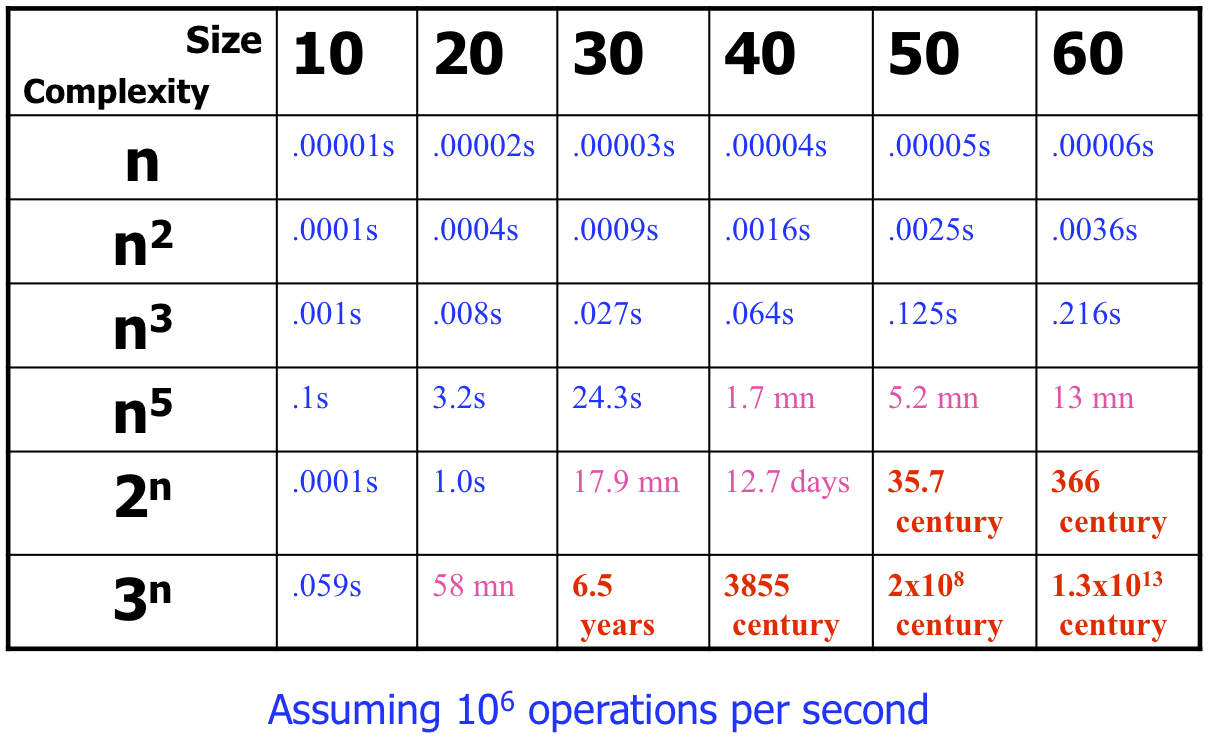
Complexity matters. For some algorithms, it matters only for large data sets. For others, it matters almost regardless of the size of the data.
Ways other than mathematical analysis to understand the complexity of an algorithm:
Example of visualization: Sergey's VisualSort application.
Not graded. Violates my goal, which is one-week turnaround.
Number 1. It's hard to come up with a new algorithm for some problems...
Number 2. Not in place -- two extra arrays! Not stable -- try it with two 13s and see where they end up.
Number 3. None of us are lawyers (are we?). But we all have intuitions, especially as creators of programs and algorithms. Think them through. Work them out.
The law is unsettled. As it stands, we cannot patent "scientific facts" or "mathematical expressions". We can patent other algorithms, if they are implemented as programs.
To me, this distinction betrays a fundamental misunderstanding of algorithms relative to "mathematical expression". I'm not comfortable with most software patents, especially those that are algorithmic in nature.