April 21, 2024 12:41 PM
The Truths We Express To Children Are Really Our Hopes
In her Conversation with Tyler, scholar Katherine Rundell said something important about the books we give our children:
Children's novels tend to teach the large, uncompromising truths that we hope exist. Things like love will matter, kindness will matter, equality is possible. I think that we express them as truths to children when what they really are are hopes.
This passage immediately brought to mind Marick's Law: In software, anything of the form "X's Law" is better understood by replacing the word "Law" with "Fervent Desire". (More on this law below.)
While comments on different worlds, these two ideas are very much in sync. In software and so many other domains, we coin laws that are really much more expressions of our aspiration. This no less true in how we interact with young people.
We usually think that our job is to teach children the universal truths we have discovered about the world, but what we really teach them is our view of how the world can or should be. We can do that by our example. We can also do that with good books.
But aren't the universal truths in our children's literature true? Sometimes, perhaps, but not all of them are true all of the time, or for all people. When we tell stories, we are describing the world we want for our children, and giving them the hope, and perhaps the gumption, to make our truths truer than we ourselves have been able to.
I found myself reading lots of children's books and YA fiction when my daughters were young: to them, and with them, and on their recommendation. Some of them affected me enough that I quoted them in blog posts. There is so many good books for our youth in the library: honest, relevant to their experiences, aspirational, exemplary. I concur in Rundell's suggestion that adults should read children's fiction occasionally, both for pleasure and "for the unabashed politics of idealism that they have".
More on Marick's Law and Me
I remember posting Marick's Law on this blog in October 2015, when I wanted to share a link to it with Mike Feathers. Brian had tweeted the law in 2009, but a link to a tweet didn't feel right, not at a time when the idealism of the open web was still alive. In my post, I said "This law is too important to be left vulnerable to the vagaries of an internet service, so let's give it a permanent home".
In 2015, the idea that Twitter would take a weird turn, change its name to X, and become a place many of my colleagues don't want to visit anymore seemed far-fetched. Fortunately, Brian's tweet is still there and, at least for now, publicly viewable via redirect. Even so, given the events of the last couple of years, I'm glad I trusted my instincts and gave the law a more home on Knowing and Doing. (Will this blog outlive Twitter?)
The funny thing, though, is that that wasn't its first appearance here. I found the 2015 URL for use in this post by searching for the word "fervent" in my Software category. That search also brought up a Posts of the Day post from April 2009 — the day after Brian tweeted the law. I don't remember that post now, and I guess I didn't remember it in 2015 either.
Sometimes, "Great minds think alike" doesn't require two different people. With a little forgetfulness, they can be Past Me and Current Me.
March 31, 2024 9:18 AM
A Man to Go to Work, A Man to Stay at Home
I was listening to some music from the 1970s yesterday morning while doing some academic bookkeeping. As happens occasionally, the lyrics of one of the songs jerked me out of my bureaucratic trance by echoing my subconscious:
I need to be three men in one
To get my job done
I need a thirty hour day
Two jobs with double pay
I need a man to go to work
A man to stay at home
That's William Bell in his 1977 R&B crossover hit "Tryin' to Love Two" [ YouTube ].
I love only one, truly, but... University work has been unusually busy the last couple of weeks, and now we enter April, which is always a hyperactive month on campus. Add to that regular life — tax season and plans for May travel and wanting to spend time with the one I love — and I empathize with Bell wanting to be two or three people all at once. A doppelgänger to attend all my extra meetings would certainly be welcome some days!
At times like this, though, it's good to remember how lucky I am that this is the biggest predicament I face. So: hello, April.
March 14, 2024 12:37 PM
Gene Expression
Someone sent me this image, from a slide deck they ran across somewhere:
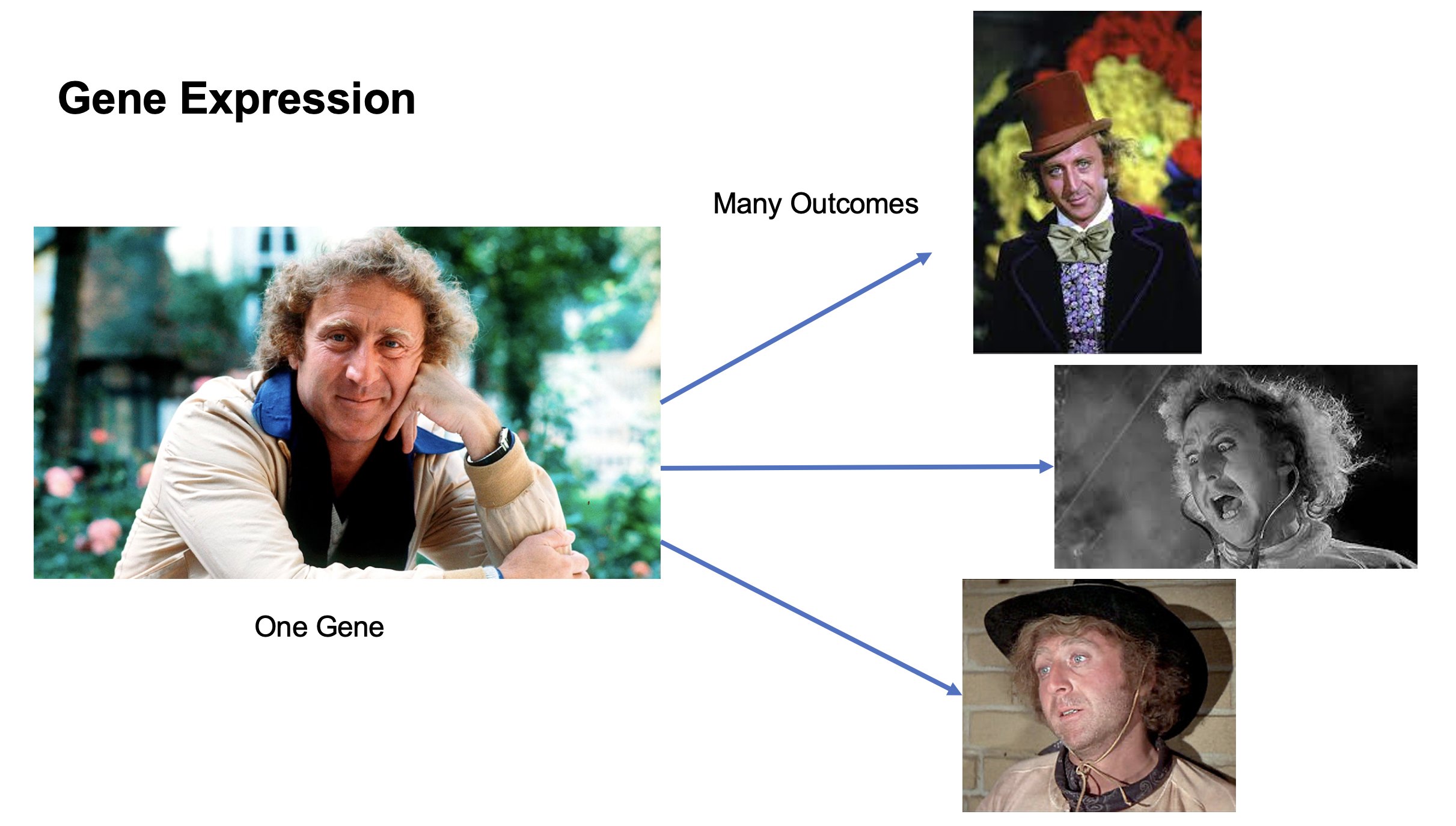
I don't know what to do with it other than to say this:
As a person named 'Eugene' and an admirer of Mr. Wilder's work, I smile every time I see it. That's a clever way to reinforce the idea of gene expression by analogy, using actors and roles.
When I teach OOP and FP, I'm always looking for simple analogies like this from the non-programming world to reinforce ideas that we are learning about in class. My OOP repertoire is pretty deep. As I teach functional programming each spring, I'm still looking for new FP analogies all the time.
~~~~~
Note: I don't know the original source of this image. If you know who created the slide, please let me know via email, Mastodon, or Twitter (all linked in the sidebar). I would love to credit the creator.
February 29, 2024 3:45 PM
Finding the Torture You're Comfortable With
At some point last week, I found myself pointed to this short YouTube video of Jerry Seinfeld talking with Howard Stern about work habits. Seinfeld told Stern that he was essentially always thinking about making comedy. Whatever situation he found himself in, even with family and friends, he was thinking about how he could mine it for new material. Stern told him that sounded like torture. Jerry said, yes, it was, but...
Your blessing in life is when you find the torture you're comfortable with.
This is something I talk about with students a lot.
Sometimes it's a current student who is worried that CS isn't for them because too often the work seems hard, or boring. Shouldn't it be easy, or at least fun?
Sometimes it's a prospective student, maybe a HS student on a university visit or a college student thinking about changing their major. They worry that they haven't found an area of study that makes them happy all the time. Other people tell them, "If you love what you do, you'll never work a day in your life." Why can't I find that?
I tell them all that I love what I do -- studying, teaching, and writing about computer science -- and even so, some days feel like work.
I don't use torture as analogy the way Seinfeld does, but I certainly know what he means. Instead, I usually think of this phenomenon in terms of drudgery: all the grunt work that comes with setting up tools, and fiddling with test cases, and formatting documentation, and ... the list goes on. Sometimes we can automate one bit of drudgery, but around the corner awaits another.
And yet we persist. We have found the drudgery we are comfortable with, the grunt work we are willing to do so that we can be part of the thing it serves: creating something new, or understanding one little corner of the world better.
I experienced the disconnect between the torture I was comfortable with and the torture that drove me away during my first year in college. As I've mentioned here a few times, most recently in my post on Niklaus Wirth, from an early age I had wanted to become an architect (the kind who design houses and other buildings, not software). I spent years reading about architecture and learning about the profession. I even took two drafting courses in high school, including one in which we designed a house and did a full set of plans, with cross-sections of walls and eaves.
Then I got to college and found two things. One, I still liked architecture in the same way as I always had. Two, I most assuredly did not enjoy the kind of grunt work that architecture students had to do, nor did I relish the torture that came with not seeing a path to a solution for a thorny design problem.
That was so different from the feeling I had writing BASIC programs. I would gladly bang my head on the wall for hours to get the tiniest detail just the way I wanted it, either in the code or in the output. When the torture ended, the resulting program made all the pain worth it. Then I'd tackle a new problem, and it started again.
Many of the students I talk with don't yet know this feeling. Even so, it comforts some of them to know that they don't have to find The One Perfect Major that makes all their boredom go away.
However, a few others understand immediately. They are often the ones who learned to play a musical instrument or who ran cross country. The pianists remember all the boring finger exercises they had to do; the runners remember all the wind sprints and all the long, boring miles they ran to build their base. These students stuck with the boredom and worked through the pain because they wanted to get to the other side, where satisfaction and joy are.
Like Seinfeld, I am lucky that I found the torture I am comfortable with. It has made this life a good one. I hope everyone finds theirs.
Posted by Eugene Wallingford | Permalink | Categories: Computing, Personal, Running, Software Development, Teaching and Learning
February 09, 2024 3:45 PM
Finding Cool Ideas to Play With
In a recent post on Computational Complexity, Bill Gasarch wrote up the solution to a fun little dice problem he had posed previously. Check it out. After showing the solution, he answered some meta-questions. I liked this one:
How did I find this question, and its answer, at random? I intentionally went to the math library, turned my cell phone off, and browsed some back issues of the journal Discrete Mathematics. I would read the table of contents and decide what article sounded interesting, read enough to see if I really wanted to read that article. I then SAT DOWN AND READ THE ARTICLES, taking some notes on them.
He points out that turning off his cell phone isn't the secret to his method.
It's allowing yourself the freedom to NOT work on a a paper for the next ... conference and just read math for FUN without thinking in terms of writing a paper.
Slack of this sort used to be one of the great attractions of the academic life. I'm not sure it is as much a part of the deal as it once was. The pace of the university seems faster these days. Many of the younger faculty I follow out in the world seem always to be hustling for the next conference acceptance or grant proposal. They seem truly joyous when an afternoon turns into a serendipitous session of debugging or reading.
Gasarch's advice is wise, if you can follow it: Set aside time to explore, and then do it.
It's not always easy fun; reading some articles is work. But that's the kind of fun many of us signed up for when we went into academia.
~~~~~
I haven't made enough time to explore recently, but I did get to re-read an old paper unexpectedly. A student came to me to discuss possible undergrad research projects. He had recently been noodling around, implementing his own neural network simulator. I've never been much of a neural net person, but that reminded of this paper on PushForth, a concatenative language in the spirit of Forth and Joy designed as part of an evolutionary programming project. Genetic programming has always interested me, and concatenative languages seem like a perfect fit...
I found the paper in a research folder and made time to re-read it for fun. This is not the kind of fun Gasarch is talking about, as it had potential use for a project, but I enjoyed digging into the topic again nonetheless.
The student looked at the paper and liked the idea, too, so we embarked on a little project -- not quite serendipity, but a project I hadn't planned to work on at the turn of the new year. I'll take it!
January 27, 2024 7:10 PM
Today in "It's not the objects; it's the messages"
Alan Kay is fond of saying that object-oriented programming is not about the objects; it's about the messages. He also looks to the biological world for models of how to think about and write computer programs.
This morning I read two things on the exercise bike that brought these ideas to mind, one from the animal kingdom and one from the human sphere.
First was a surprising little article on how an invasive ant species is making it harder for Kenyan lions to hunt zebras, with elephants playing a pivotal role in the story, too. One of the scientists behind the study said:
"We often talk about conservation in the context of species. But it's the interactions which are the glue that holds the entire system together."
It's not just the animals. It's the interactions.
Then came @jessitron reflecting on what it means to be "the best":
And then I remembered: people are people through other people. Meaning comes from between us, not within us.
It's not just the people. It's the interactions.
Both articles highlighted that we are usually better served by thinking about interactions within systems, and not simply the components of system. That way lies a more reliable approach to build robust software. Alan Kay is probably somewhere nodding his head.
The ideas in Jessitron's piece fit nicely into the software analogy, but they mean even more in the world of people that she is reflecting on. It's easy for each of us to fall into the habit of walking around the world as an I and never quite feeling whole. Wholeness comes from connection to others. I occasionally have to remind myself to step back and see my day in terms of the students and faculty I've interacted with, whom I have helped and who have helped me.
It's not (just) the people. It's the interactions.
January 21, 2024 8:28 AM
A Few Thoughts on How Criticism Affects People
The same idea popped up in three settings this week: a conversation with a colleague about student assessments, a book I am reading about women writers, and a blog post I read on the exercise bike one morning.
The blog post is by Ben Orlin at Math With Bad Drawings from a few months ago, about an occasional topic of this blog: being less wrong each day [ for example, 1 and 2 ]. This sentence hit close enough to home that I saved it for later.
We struggle to tolerate censure, even the censure of idiots. Our social instrument is strung so tight, the least disturbance leaves us resonating for days.
Perhaps this struck a chord because I'm currently reading A Room of One's Own, by Virginia Woolf. In one early chapter, Woolf considers the many reasons that few women wrote poetry, fiction, or even non-fiction before the 19th century. One is that they had so little time and energy free to do so. Another is that they didn't have space to work alone, a room of one's own. But even women who had those things had to face a third obstacle: criticism from men and women alike that women couldn't, or shouldn't, write.
Why not shrug off the criticism and soldier on? Woolf discusses just how hard that is for anyone to do. Even many of our greatest writers, including Tennyson and Keats, obsessed over every unkind word said about them or their work. Woolf concludes:
Literature is strewn with the wreckage of men who have minded beyond reason the opinions of others.
Orlin's post, titled Err, and err, and err again; but less, and less, and less, makes an analogy between the advance of scientific knowledge and an infinite series in mathematics. Any finite sum in the series is "wrong", but if we add one more term, it is less wrong than the previous sum. Every new term takes us closer to the perfect answer.

He then goes on to wonder whether the same is, or could be, true of our moral development. His inspiration is American psychologist and philosopher William James. I have mentioned James as an inspiration myself a few times in this blog, most explicitly in Pragmatism and the Scientific Spirit, where I quote him as saying that consciousness is "not a thing or a place, but a process".
Orlin connects his passage on how humans receive criticism to James's personal practice of trying to listen only to the judgment of ever more noble critics, even if we have to imagine them into being:
"All progress in the social Self," James says, "is the substitution of higher tribunals for lower."
If we hold ourselves to a higher, more noble standard, we can grow. When we reach the next plateau, we look for the next higher standard to shoot for. This is an optimistic strategy for living life: we are always imperfect, but we aspire to grow in knowledge and moral development by becoming a little less wrong each step of the way. To do so, we try to focus our attention on the opinions of those whose standard draws us higher.
Reading James almost always leaves my spirit lighter. After Orlin's post, I feel a need to read The Principles of Psychology in full.
These two threads on how people respond to criticism came together when I chatted with a colleague this week about criticism from students. Each semester, we receive student assessments of our courses, which include multiple-choice ratings as well as written comments. The numbers can be a jolt, but their effect is nothing like that of the written comments. Invariably, at least one student writes a negative response, often an unkind or ungenerous one.
I told my colleague that this is recurring theme for almost every faculty member I have known: Twenty-nine students can say "this was a good course, and I really like the professor", but when one student writes something negative... that is the only comment we can think about.
The one bitter student in your assessments is probably not the ever more noble critic that James encourages you to focus on. But, yeah. Professors, like all people, are strung pretty tight when it comes to censure.
Fortunately, talking to others about the experience seems to help. And it may also remind us to be aware of how students respond to the things we say and do.
Anyway, I recommend both the Orlin blog post and Woolf's A Room of One's Own. The former is a quick read. The latter is a bit longer but a smooth read. Woolf writes well, and once my mind got on the book's wavelength, I found myself engaged deeply in her argument.
January 06, 2024 10:41 AM
end.

My social media feed this week has included many notes and tributes on the passing of Niklaus Wirth, including his obituary from ETH Zurich, where he was a professor. Wirth was, of course, a Turing Award winner for his foundational work designing a sequence of programming languages.
Wirth's death reminded me of
END DO,
my post on the passing of John Backus, and before that
a post
on the passing of Kenneth Iverson. I have many fond memories related
to Wirth as well.
Pascal
Pascal was, I think, the fifth programming language I learned. After that, my language-learning history starts to speed up and blur. (I do think APL and Lisp came soon after.)
I learned BASIC first, as a junior in high school. This ultimately changed the trajectory of my life, as it planted the seeds for me to abandon a lifelong dream to be an architect.
Then at university, I learned Fortran in CS 1, PL/I in Data Structures (you want pointers!), and IBM 360/370 assembly language in a two-quarter sequence that also included JCL. Each of these language expanded my mind a little.
Pascal was the first language I learned "on my own". The fall of my junior year, I took my first course in algorithms. On Day 1, the professor announced that the department had decided to switch to Pascal in the intro course, so that's what we would use in this course.
"Um, prof, that's what the new CS majors are learning. We know Fortran and PL/I." He smiled, shrugged, and turned to the chalkboard. Class began.
After class, several of us headed immediately to the university library, checked out one Pascal book each, and headed back to the dorms to read. Later that week, we were all using Pascal to implement whatever classical algorithm we learned first in that course. Everything was fine.
I've always treasured that experience, even if it was little scary for a week or so. And don't worry: That professor turned out to be a good guy with whom I took several courses. He was a fellow chess player and ended up being the advisor on my senior project: a program to perform the Swiss system commonly used to run chess tournaments. I wrote that program in... Pascal. Up to that point, it was the largest and most complex program I had ever written solo. I still have the code.
The first course I taught as a tenure-track prof was my university's version of CS 1 -- using Pascal.
Fond memories all. I miss the language.
Wirth sightings in this blog
I did a quick search and found that Wirth has made an occasional appearance in this blog over the years.
• January 2006: Just a Course in Compilers
This was written at the beginning of my second offering of our compiler course, which I have taught and written about many times since. I had considered using as our textbook Wirth's Compiler Construction, a thin volume that builds a compiler for a subset of Wirth's Oberon programming language over the course of sixteen short chapters. It's a "just the facts and code" approach that appeals to me most days.
I didn't adopt the book for several reasons, not least of which that at the time Amazon showed only four copies available, starting at $274.70 each. With two decades of experience teaching the course now, I don't think I could ever really use this book with my undergrads, but it was a fun exercise for me to work through. It helped me think about compilers and my course.
Note: A PDF of Compiler Construction has been posted on the
web for many years, but every time I link to it, the link ultimately
disappears. I decided to mirror the files locally, so that the link
will last as long as this post lasts:
[
Chapters 1-8
|
Chapters 9-16
]
• September 2007: Hype, or Disseminating Results?
... in which I quote Wirth's thoughts on why Pascal spread widely in the world but Modula and Oberon didn't. The passage comes from a short historical paper he wrote called "Pascal and its Successors". It's worth a read.
• April 2012: Intermediate Representations and Life Beyond the Compiler
This post mentions how Wirth's P-code IR ultimately lived on in the MIPS compiler suite long after the compiler which first implemented P-code.
• July 2016: Oberon: GoogleMaps as Desktop UI
... which notes that the Oberon spec defines the language's desktop as "an infinitely large two-dimensional space on which windows ... can be arranged".
• November 2017: Thousand-Year Software
This is my last post mentioning Wirth before today's. It refers to the same 1999 SIGPLAN Notices article that tells the P-code story discussed in my April 2012 post.
I repeat myself. Some stories remain evergreen in my mind.
The Title of This Post
I titled my post on the passing of John Backus END DO
in homage to his intimate connection to Fortran. I wanted to do something
similar for Wirth.
Pascal has a distinguished sequence to end a program:
"end.". It seems a
fitting way to remember the life of the person who created it and who
gave the world so many programming experiences.
December 31, 2023 1:35 PM
"I Want to Find Something to Learn That Excites Me"
In his year-end wrap-up, Greg Wilson writes:
I want to find something to learn that excites me. A new musical instrument is out because of my hand; I've thought about reviving my French, picking up some Spanish, diving into Postgres or machine learningn (yeah, yeah, I know, don't hate me), but none of them are making my heart race.
What he said. I want to find something to learn that excites me.
I just spent six months immersed in learning more about HTML, CSS, and JavaScript so that I could work with novice web developers. Picking up that project was one part personal choice and one part professional necessity. It worked out well. I really enjoyed studying the web development world and learned some powerful new tools. I will continue to use them as time and energy permit.
But I can't say that I am excited enough by the topic to keep going in this area. Right now, I am still burned out from the semester on a learning treadmill. I have a followup post to my early reactions about the course's JavaScript unit in the hopper, waiting for a little desire to finish it.
What now? There are parallels between my state and Wilson's.
- After my first-ever trip to Europe in 2019, for a Dagstuhl seminar (brief mention here), my wife and I talked about a return trip, with a focus this time on Italy. Learning Italian was part of the nascent plan. Then came COVID, along with a loss of energy for travel. I still have learning Italian in my mind.
- In the fall of 2020, the first full semester of the pandemic, I taught a database course for the first time (bookend posts here and here). I still have a few SQL projects and learning goals hanging around from that time, but none are calling me right now.
- LLMs are the main focus of so many people's attention these days, but they still haven't lit up me up. In some ways, I envy David Humphrey, who fell in love with AI this year. Maybe something about LLMs will light me up one of these days. (As always, you should read David's stuff. He does neat work and shares it with the world.)
Unlike Wilson, I do not play a musical instrument. I did, however, learn a little basic piano twenty-five years ago when I was a Suzuki piano parent with my daughters. We still have our piano, and I harbor dreams of picking it back up and going farther some day. Right now doesn't seem to be that day.
I have several other possibilities on the back burner, particularly in the area of data analytics. I've been intrigued by the work on data-centric computing in education being done by Kathi Fisler and Shriram Krishnamurthi have been at Brown. I also will be reading a couple of their papers on program design and plan composition in the coming weeks as I prepare for my programming languages course this spring. Fisler and Krishnamurthi are coming at these topics from the side of CS education, but the topics are also related to my grad-school work in AI. Maybe these papers will ignite a spark.
Winter break is coming to an end soon. Like others, I'm thinking about 2024. Let's see what the coming weeks bring.
November 24, 2023 12:17 PM
And Then Came JavaScript
It's been a long time again between posts. That seems to be the new normal. On top of that, though, teaching web development this fall for the first time has been soaking up all of my free hours in the evenings and over the weekends, which has left me little time to be sad about not blogging. I've certainly been writing plenty of text and a bit of code.
The course started off with a lot of positive energy. The students were excited to learn HTML and CSS. I made a few mistakes in how I organized and presented topics, but things went pretty well. By all accounts, students seemed to enjoy what they were learning and doing.
And then came JavaScript.
Well, along came real computer programming. It could have been Python or some other language, I think, but the transition to writing programs, even short bits of code, took the wind out of the students' excitement.
I was prepared for the possibility that the mood of the course would change when we shifted from CSS to JavaScript. A previous offering of the course had encountered a similar obstacle. Learning to program is a challenge. I'm still not convinced that learning to program is that much harder than a lot of things people learn to do, but it does take time.
As I prepared for the course last summer, I saw so many different approaches to teaching JavaScript for web development. Many assumed a lot of HTML/CSS/DOM background, certainly more than my students had picked up in six weeks. Others assumed programming experience most of my students didn't have, even when the approach said 'no experience necessary!'. So I had to find a middle path.

My main source of inspiration in the first half of the course was David Humphrey's WEB 222 course, which was explicitly aimed at an audience of CS students with programming experience. So I knew that I had to do something different with my students, even as I used his wonderful course materials whenever I could.
My department had offered this course once many years ago, aimed at much the same kind of audience as mine, and the instructor — a good friend — shared all of his materials. I used that offering as a primary source of ideas for getting started with JavaScript, and I occasionally adapted examples for use in my class.
The results were not ideal. Students don't seem to have enjoyed this part of the course much at all. Some acknowledged that to me directly. Even the most engaged students seemed to lose a bit of their energy for the course. Performance also sagged. Based on homework solutions and a short exam, I would say that only one student has achieved the outcomes I had originally outlined for this unit.
I either expected too much or did not do a good enough job helping students get to where I wanted them to be.
I have to do better next time.
But how?
Programming isn't as hard as some people tell us, but most of us can't learn to do it in five or six weeks, at least not enough to become very productive. We don't expect students to master all of CSS or even HTML in such a short time, so we can't expect them to master JavaScript either. The difference is that there seems to be a smooth on-ramp for learning HTML and CSS on the way to mastery, while JavaScript (or any other programming language) presents a steep climb, with occasional plateaus.
For now, I am thinking that the key to doing better is to focus on an even narrower set of concepts and skills.
If people starting from scratch can't learn all of JavaScript in five or six weeks, or even enough to be super-productive, what useful skills can they learn in that time? For this course I trimmed down the set of topics that we might cover in an intro CS considerably, but I think I need to trim even more and — more importantly — choose topics and examples that are even more embedded in the act of web development.
Earlier this week, a sudden burst of thought outlined something like this:
-
document.querySelector()to select an element in a page - simple assignment statements to modify
innerText,innerHTML, and various style attributes - parameterizing changes to an element to create a function
-
document.querySelectorAll()to select collections of elements in a page -
forEachto process every element in a collection - guarded actions to select items in the collection using
ifstatements, withoutelseclauses
That is a lot to learn in five weeks! Even so, it cuts way back on several topics I tried cover this time, such as a more general discussion of objects, arrays, and boolean values, and a deeper look at the DOM. And it eliminates even mentioning several topics altogether:
-
if-elsestatements -
whilestatements - counted
forloops and, more generally, map-like behavior - any fiddling with numbers and arithmetic, which are often used
to learn assignment statements,
ifstatements, and function
There are so many things a programmer can't do without these concepts, such as writing an indefinite data validation loop or really understanding what's going on in the DOM tree. But trying to cover all of those topics too did not result in students being able to do them either! I think it left them confused, with so many new ideas jumbled in their minds, and a general dissatisfaction at being unable to use JavaScript effectively.
Of course I would want to build hooks into the course for students who want to go deeper and are ready to do so. There is so much good material on the web for people who are ready for more. Providing more enriched opportunities for advanced students is easier than designing learning opportunities for beginners.
Can something like this work?
I won't know for a while. It will be at least a year before I teach this course again. I wish I could teach it again sooner, so that I could try some of my new ideas and get feedback on them sooner. Such is the curse of a university calendar and once-yearly offerings.
It's too late to make any big changes in trajectory this semester. We have only two weeks after the current one-week Thanksgiving break. Next week, we will focus on input forms (HTML), styling (CSS), and a little data validation (HTML+JavaScript). I hope that this return to HTML+CSS helps us end the course on a positive note. I'd like for students to finish with a good feeling about all they have learned and now can do.